题目内容
10.不等式组$\left\{\begin{array}{l}{3x+4≥0}\\{\frac{1}{2}x-24≤1}\end{array}\right.$的所有整数解的积为0.分析 先分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的所有整数解相乘即可求解.
解答 解:$\left\{\begin{array}{l}{3x+4≥0①}\\{\frac{1}{2}x-24≤1②}\end{array}\right.$,
解不等式①得:x$≥-\frac{4}{3}$,
解不等式②得:x≤50,
∴不等式组的整数解为-1,0,1…50,
所以所有整数解的积为0,
故答案为:0.
点评 本题考查的是解一元一次不等式组及求一元一次不等式组的整数解,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
18.计算3+(-3)的结果是( )
| A. | 6 | B. | -6 | C. | 1 | D. | 0 |
15.关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
5.等腰梯形底角为α,以腰长为直径作圆与另一腰切于M,交较长底边AB于E,则$\frac{BE}{AE}$的值为( )
| A. | 2sinαcosα | B. | sinα | C. | cosα | D. | cos2α |
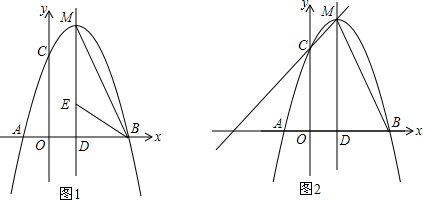
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: