题目内容
6.解下列各题①$[{1\frac{2}{3}-({\frac{1}{3}-\frac{1}{6}+\frac{5}{12}})×2.4}]÷5$.
②${({-3})^2}-{({1\frac{1}{2}})^3}×\frac{2}{9}-6÷{|{-\frac{2}{3}}|^3}$.
分析 ①先根据乘法分配律计算出括号中的数,再算除法即可;
②先算乘方,再算乘除,最后算加减即可.
解答 解:①原式=[1$\frac{2}{3}$-$\frac{1}{3}$×2.4+$\frac{1}{6}$×2.4-$\frac{5}{12}$×2.4]÷5
=(1$\frac{2}{3}$-0.8+0.4-1)÷5
=(1$\frac{2}{3}$-1.4)÷5
=$\frac{4}{15}$×$\frac{1}{5}$
=$\frac{4}{75}$;
②原式=9-$\frac{27}{8}$×$\frac{2}{9}$-6÷$\frac{8}{27}$
=9-$\frac{3}{4}$-$\frac{81}{4}$
=9-($\frac{3}{4}$+$\frac{81}{4}$)
=9-21
=-12.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的顺序是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
1.已知x1、x2是一元二次方程x2+2ax+b=0的两个根,且x1+x2=-3,x1x2=-1,则a、b的值分别是( )
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=$\frac{3}{2}$,b=-1 | D. | a=-$\frac{3}{2}$,b=1 |
18.下列各式从左到右的变形是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | x2-4x+5=x(x-4)+5 | C. | 3x2-6x=-6x+3x2 | D. | 8a-4a2-4=-4(a-1)2 |
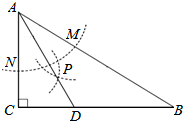 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )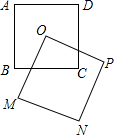 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.