题目内容
1．化简与计算（1）（$\sqrt{3}$-2）0+（$\frac{1}{3}$）-1+4cos30°-|-$\sqrt{12}$|．
（2）先化简，再求值：$\frac{a-3}{2a-4}$÷（$\frac{5}{a-2}$-a-2），其中a=$\sqrt{3}$-3．
分析 （1）原式第一项利用零指数幂法则计算，第二项利用负整数指数幂法则计算，第三项利用特殊角的三角函数值计算，最后一项利用绝对值的代数意义化简，计算即可得到结果；
（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．
解答 解：（1）原式=1+3+2$\sqrt{3}$-2$\sqrt{3}$=4；
（2）原式=$\frac{a-3}{2（a-2）}$÷$\frac{5-（a+2）（a-2）}{a-2}$=-$\frac{a-3}{2（a-2）}$•$\frac{a-2}{（a+3）（a-3）}$=-$\frac{1}{2a+6}$，
当a=$\sqrt{3}$-3时，原式=-$\frac{\sqrt{3}}{6}$．
点评 此题考查了分式的化简求值，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
11．如果x=2是关于x的方程3-2x=x+a的解，那么a的值应是（ ）
| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
12．
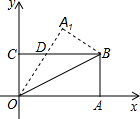如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）
如图，在平面直角坐标系中，将矩形OABC沿对角线OB对折，使点A（$\sqrt{3}$，0）落在点A1处，已知点B的坐标是（$\sqrt{3}$，1），则点A1的坐标是（ ）| A． | （$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$） | B． | （$\frac{{\sqrt{3}}}{2}$，$\frac{3}{2}$） | C． | （$\frac{{\sqrt{3}}}{2}$，2） | D． | （$\frac{3}{2}$，$\frac{{\sqrt{3}}}{2}$） |
16．用一个半径为30cm，面积为300π cm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为（ ）
| A． | 5cm | B． | 10cm | C． | 20cm | D． | 5πcm |
6．下列函数中，y是x的反比例函数的是（ ）
| A． | y=2x+1 | B． | $y=\frac{1}{3x}$ | C． | $y=\frac{1}{x-5}$ | D． | y=$\frac{2}{{x}^{2}}$ |
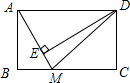如图，矩形ABCD中，AB=4，AD=9，点M在BC上，且BM：MC=1：2，DE⊥AM于点E，求DE的长为$\frac{36}{5}$．