题目内容
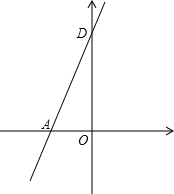 如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0).
如图,已知直线y=2x+6与x轴、y轴分别交于A、D两点,抛物线y=ax2+bx+2(a≠0)经过点A和点B(1,0).(1)求抛物线的解析式;
(2)在线段AD上取一点F(点F不与点A重合).过点F作x轴的垂线交抛物线于点G、交x轴于点H.当FG=GH时,求点H的坐标;
(3)设抛物线的对称轴与直线AD交于点E,抛物线与y轴的交点为C,点M在线段AB上,当△AEM与△BCM相似时,求点M的坐标.
考点:二次函数综合题
专题:
分析:(1)根据函数值,可得相应自变量的值,根据待定系数法,可得函数解析式;
(2)根据自变量的值,可得相应函数值,根据FG=GH,可得关于a的方程,解方程,可得答案;
(3)根据相似三角形的性质,可得关于b的方程,解方程,可得答案.
(2)根据自变量的值,可得相应函数值,根据FG=GH,可得关于a的方程,解方程,可得答案;
(3)根据相似三角形的性质,可得关于b的方程,解方程,可得答案.
解答:解:(1)当y=0时,2x+6=0.解得x=-3,即A(-3,0),
由抛物线y=ax2+bx+2(a≠0)经过点A(-3,0)和点B(1,0),得
,
解得
.
故抛物线为y=-
x2-
x+2;
(2)设H点的坐标为(a,0),F(a,2a+6),G(a,-
a2-
a+2).
由FG=GH,得
2a+6=2(-
a2-
a+2).
化简,得2a2+7a+3=0.
解得a=-
,a=-3(不符合题意要舍去),
点H的坐标(-
,0);
(3)设M点坐标为(b,0),AM=b+3,BM=1-b,
抛物线的对称轴与直线AD交于点E,抛物线与y轴的交点为C,得
E(-1,4),C(0,2).
由勾股定理,得
AE=2
,BC=
.
当△AEM∽△BCM时,
=
,即
=
.
化简,得3b=-1,解得b=-
,即M(-
,0);
当△AEM∽△BMC时,
=
,即
=
,
化简,得b2+2b+7=0.实数b不存在;
综上所述:M(-
,0).
由抛物线y=ax2+bx+2(a≠0)经过点A(-3,0)和点B(1,0),得
|
解得
|
故抛物线为y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)设H点的坐标为(a,0),F(a,2a+6),G(a,-
| 2 |
| 3 |
| 4 |
| 3 |
由FG=GH,得
2a+6=2(-
| 2 |
| 3 |
| 4 |
| 3 |
化简,得2a2+7a+3=0.
解得a=-
| 1 |
| 2 |
点H的坐标(-
| 1 |
| 2 |
(3)设M点坐标为(b,0),AM=b+3,BM=1-b,
抛物线的对称轴与直线AD交于点E,抛物线与y轴的交点为C,得
E(-1,4),C(0,2).
由勾股定理,得
AE=2
| 5 |
| 5 |
当△AEM∽△BCM时,
| AE |
| BC |
| AM |
| BM |
2
| ||
|
| b+3 |
| 1-b |
化简,得3b=-1,解得b=-
| 1 |
| 3 |
| 1 |
| 3 |
当△AEM∽△BMC时,
| AE |
| BM |
| AM |
| BC |
2
| ||
| 1-b |
| b+3 | ||
|
化简,得b2+2b+7=0.实数b不存在;
综上所述:M(-
| 1 |
| 3 |
点评:本题考查了二次函数综合题,(1)利用了待定系数法求函数解析式,(2)利用了线段中点的性质,(3)利用了相似三角形的性质.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
化简x-2(x-y)的结果是( )
| A、-x+y | B、-x-y |
| C、-x+2y | D、-x-2y |
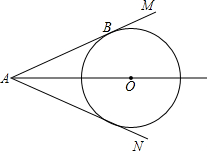 已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.
已知,如图,点O是的角∠MAN平分线上任意一点,以点O为圆心的圆切AM于点B.