题目内容
 如图,等边△ABC中,点M在AC边上,点N在CB的延长线上,且AM=BN,MC=nAM,线段MN交AB交于P点.
如图,等边△ABC中,点M在AC边上,点N在CB的延长线上,且AM=BN,MC=nAM,线段MN交AB交于P点.(1)当n=1时,求
| PM |
| PN |
| PA |
| PB |
(2)当n=2时,求证:PA=2PB;
(3)当n为何值时,PA=5PB?
考点:相似三角形的判定与性质,等边三角形的性质
专题:常规题型
分析:作MD∥BC,交AB于D,易证△DMP≌△BNP;
(1)根据△DMP≌△BNP即可求得
和
的值;
(2)取n=2,即可求得
=
,即可解题;
(3)当PA=5PB时,可求得
=
=2,即可解题.
(1)根据△DMP≌△BNP即可求得
| PM |
| PN |
| AP |
| BP |
(2)取n=2,即可求得
| BP |
| AP |
| 1 |
| 2 |
(3)当PA=5PB时,可求得
| AM |
| MC |
| AD |
| BD |
解答:解:如图,作MD∥BC,交AB于D,
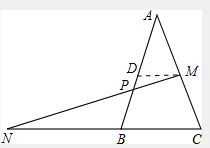
则AM=DM=AD,
∴△ADM∽△ABC,
又∵AM=BN,
∴BN=DM,
在△DMP和△BNP中,
,
∴△DMP≌△BNP(ASA),
∴PM=PN,PD=PB,
∴
=1,
(1)当n=1时(即点M是AC中点),AM=DM=BN,
∴PB=
,
又AD=BD=
,
∴
=4,
∴
=3,
(2)当n=2时
=
=
,
=
,
=
,
∴
=
,
即AP=2PB;
(3)当PA=5PB时,
=
,
=
,
=
=2,
∴n=
.

则AM=DM=AD,
∴△ADM∽△ABC,
又∵AM=BN,
∴BN=DM,
在△DMP和△BNP中,
|
∴△DMP≌△BNP(ASA),
∴PM=PN,PD=PB,
∴
| PM |
| PN |
(1)当n=1时(即点M是AC中点),AM=DM=BN,
∴PB=
| BD |
| 2 |
又AD=BD=
| AB |
| 2 |
∴
| AB |
| BP |
∴
| AP |
| BP |
(2)当n=2时
| AD |
| AB |
| AM |
| AC |
| 1 |
| 3 |
| BD |
| AB |
| 2 |
| 3 |
| BP |
| AB |
| 1 |
| 3 |
∴
| BP |
| AP |
| 1 |
| 2 |
即AP=2PB;
(3)当PA=5PB时,
| PB |
| AB |
| 1 |
| 6 |
| BD |
| AB |
| 1 |
| 3 |
| AM |
| MC |
| AD |
| BD |
∴n=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了相似三角形的判定,考查了全等三角形对应边相等的性质,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
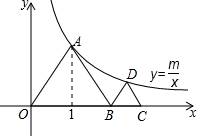 如图,边长为2的等边三角形AOB的顶点在反比例函数y=
如图,边长为2的等边三角形AOB的顶点在反比例函数y=| m |
| x |
A、
| ||||||
B、
| ||||||
C、2
| ||||||
D、2
|
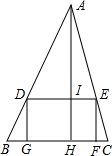 如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.
如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.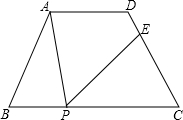 如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.
如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长. 如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC.
如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC.