题目内容
15.已知2是x的立方根,且(y-2z+5)2+$\sqrt{z-3}$=0,求$\root{3}{x+{y}^{3}+{z}^{3}-9}$的值.分析 首先利用立方根的定义以及偶次方的性质和二次根式的性质得出x,y,z的值,进而代入求出即可.
解答 解:∵2是x的立方根,
∴x=8,
∵(y-2z+5)2+$\sqrt{z-3}$=0,
∴$\left\{\begin{array}{l}{y-2z+5=0}\\{z-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{y=1}\\{z=3}\end{array}\right.$,
∴$\root{3}{x+{y}^{3}+{z}^{3}-9}$=$\root{3}{8+1+27-9}$=3.
点评 此题主要考查了立方根的定义以及偶次方的性质和二次根式的性质,得出x,y,z的值是解题关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
3.计算$\sqrt{36}$的结果是( )
| A. | 6 | B. | ±6 | C. | -6 | D. | 36 |
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.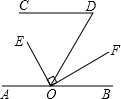 已知:AB∥CD,OE平分∠AOD,OF⊥OE于O,∠D=60°,则∠BOF=30°.
已知:AB∥CD,OE平分∠AOD,OF⊥OE于O,∠D=60°,则∠BOF=30°. 如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
如图,三条直线交于同一点,则∠1+∠2+∠3=180°. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.