题目内容
4.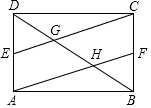 矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.求证:(1)四边形AFCE是平行四边形;
(2)EG=FH.
分析 (1)根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)可证明EG和FH所在的△DEG、△BFH全等即可.
解答 解:
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE=$\frac{1}{2}$AD,CF=$\frac{1}{2}$BC,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵AB∥CD,
∴∠EDG=∠FBH,
在△DEG和△BFH中
$\left\{\begin{array}{l}{∠DGE=∠BHF}\\{∠EDG=∠FBH}\\{DE=BF}\end{array}\right.$,
∴△DEG≌△BFH(AAS),
∴EG=FH.
点评 本题考查了矩形的性质、平行四边形的判断和性质以及全等三角形的判断和性质,熟记矩形的各种性质是解题的关键.

练习册系列答案
相关题目
12.已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
| A. | (1,-5) | B. | (3,-13) | C. | (2,-8) | D. | (4,-20) |
19.5月14-15日“一带一路”论坛峰会在北京隆重召开,促进了我国与世界各国的互联互通互惠,“一带一路”地区覆盖总人数约为44亿人,44亿这个数用科学记数法表示为( )
| A. | 4.4×108 | B. | 4.4×109 | C. | 4×109 | D. | 44×108 |
16.点A(1,y1)、B(3,y2)是反比例函数y=$\frac{9}{x}$图象上的两点,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
15.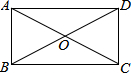 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 5cm |
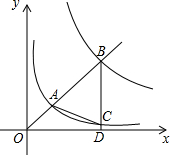 如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.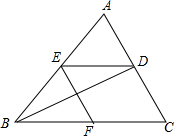 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.
如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.