Question

3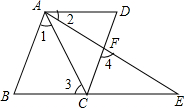．已知：如图，AB∥CD，∠1=∠2，∠3=∠4．
（1）求证：AD∥BE；
（2）若∠B=∠3=2∠2，求∠D的度数．

Answer 1

分析 （1）根据平行线的性质，由AB∥CD得到∠1=∠ACD，则利用三角形外角性质得∠BCD=∠4+∠E，加上∠3=∠4，则∠1=∠E，利用∠1=∠2得到∠2=∠E，然后根据平行线的判定即可得到结论；
（2）利用∠B=∠3=2∠2，∠1=∠2，再根据三角形内角和定理可计算出∠1=36°，则∠B=2∠1=72°，然后根据平行线的性质由AB∥CD得到∠DCE=∠B=72°，再由AD∥BE得到∠D=∠DCE=72°．

解答 （1）证明：∵AB∥CD，
∴∠1=∠ACD，
∵∠BCD=∠4+∠E，
∵∠3=∠4，
∴∠1=∠E，
∵∠1=∠2，
∴∠2=∠E，
∴AD∥BE；
（2）解：∵∠B=∠3=2∠2，∠1=∠2，
∴∠B=∠3=2∠1，
∵∠B+∠3+∠1=180°，
即2∠1+2∠1+∠1=180°，解得∠1=36°，
∴∠B=2∠1=72°，
∵AB∥CD，
∴∠DCE=∠B=72°，
∵AD∥BE，
∴∠D=∠DCE=72°．

点评 本题考查了平行线的判定与性质：平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．