题目内容
6.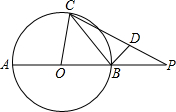 如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanα•tanβ=$\frac{1}{3}$.
如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanα•tanβ=$\frac{1}{3}$.
分析 首先连接AC,易得∠A=β,由AB是⊙O的直径,可表示出tanβ,又由BD垂直于弦BC,可表示出tanα,BD∥AC,证得△PBD∽△PAC,然后由相似三角形的对应边成比例,求得答案.
解答  证明:连接AC,则∠A=$\frac{1}{2}$∠POC=β,
证明:连接AC,则∠A=$\frac{1}{2}$∠POC=β,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴tanβ=$\frac{BC}{AC}$,
∵BD垂直于弦BC,
即DB⊥BC,
∴tanα=$\frac{BD}{BC}$,BD∥AC,
∴tana•tanβ=$\frac{BD}{BC}$•$\frac{BC}{AC}$=$\frac{BD}{AC}$,
∴∠DBP=∠A,
又∵∠P=∠P,
∴△PBD∽△PAC,
∴$\frac{BD}{AC}$=$\frac{PB}{PA}$,
∵PB=0B=OA,
∴$\frac{PB}{PA}$=$\frac{1}{3}$,
∴tana•tanβ=$\frac{1}{3}$.
点评 此题考查了相似三角形的判定与性质、圆周角定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
1.下列满足两根之和为2的一元二次方程的方程是( )
| A. | x2-2x+4=0 | B. | x2-2x-1=0 | C. | 2x2-2x-5=0 | D. | x2+2x-1=0 |
15.数1425万平方米,用科学记数法表示为( )平方米.
| A. | 1.425×108 | B. | 1.425×107 | C. | 14.25×106 | D. | 1425×104 |
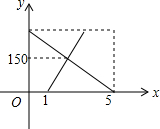 一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.
一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.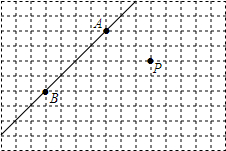 在如图所示的方格纸上,只用直尺画图.
在如图所示的方格纸上,只用直尺画图. 如图,已知△ABC,请作出△ABC关于x轴对称的图形.并写出A、B、C关于x轴对称的点坐标.
如图,已知△ABC,请作出△ABC关于x轴对称的图形.并写出A、B、C关于x轴对称的点坐标.