题目内容
 如图,在△ABC中,AB=10,△ABC的角平分线AD的长为8,BD=6,求AC的长.
如图,在△ABC中,AB=10,△ABC的角平分线AD的长为8,BD=6,求AC的长.考点:勾股定理的逆定理,全等三角形的判定与性质
专题:计算题
分析:在三角形ABD中,利用勾股定理的逆定理判断出三角形ABD为直角三角形,得到一对直角相等,再由AD为角平分线得到一对角相等,再由AD为公共边,利用ASA得到三角形ABD与三角形ACD全等,利用全等三角形的对应边相等即可求出AC的长.
解答:解:在△ABD中,AD2+BD2=82+62=100,AB2=102=100,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADB=∠ADC,
∵AD为△ABC的平分线,
∴∠BAD=∠CAD,
在△ADB和△ADC中,
,
∴△ADB≌△ADC(ASA),
∴AC=AB=10.
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADB=∠ADC,
∵AD为△ABC的平分线,
∴∠BAD=∠CAD,
在△ADB和△ADC中,
|
∴△ADB≌△ADC(ASA),
∴AC=AB=10.
点评:此题考查了勾股定理的逆定理,以及全等三角形的判定与性质,熟练掌握勾股定理的逆定理是解本题的关键.

练习册系列答案
相关题目
 如图,水平放置的空心圆柱体的主视图为( )
如图,水平放置的空心圆柱体的主视图为( )A、 |
B、 |
C、 |
D、 |
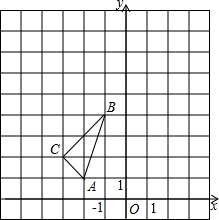 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).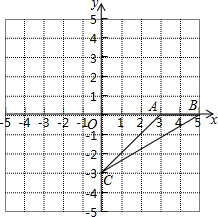 在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.
在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.