题目内容
观察下列各式:
①4×1×2+1=(1+2)2;②4×2×3+1=(2+3)2;③4×3×4+1=(3+4)2…
(1)根据你观察、归纳、发现的规律,写出4×2012×2013+1可以看成哪个数的平方?
(2)试猜想第n个等式,并通过计算验证它是否成立.
(3)利用前面的规律,将4(
x2+x)(
x2+x+1)+1改写成完全平方形式.
①4×1×2+1=(1+2)2;②4×2×3+1=(2+3)2;③4×3×4+1=(3+4)2…
(1)根据你观察、归纳、发现的规律,写出4×2012×2013+1可以看成哪个数的平方?
(2)试猜想第n个等式,并通过计算验证它是否成立.
(3)利用前面的规律,将4(
| 1 |
| 2 |
| 1 |
| 2 |
考点:规律型:数字的变化类,完全平方式
专题:
分析:(1)根据已知的三个等式,发现规律:等式左边是序号数与比序号数大1的两个正整数积的4倍与1的和,等式右边是序号数与比序号数大1的两个正整数的和的平方,由此得出4×2012×2013+1可以看成2012与2013这两个正整数的和的平方;
(2)猜想第n个等式为4n(n+1)+1=(n+n+1)2=(2n+1)2,运用多项式的乘法法则计算验证即可;
(3)利用前面的规律,可知4(
x2+x)(
x2+x+1)+1=(
x2+x+
x2+x+1)2=(x2+2x+1)2=(x+1)4.
(2)猜想第n个等式为4n(n+1)+1=(n+n+1)2=(2n+1)2,运用多项式的乘法法则计算验证即可;
(3)利用前面的规律,可知4(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)根据观察、归纳、发现的规律,得到4×2012×2013+1=(2012+2013)2=40252;
(2)猜想第n个等式为4n(n+1)+1=(2n+1)2,理由如下:
∵左边=4n(n+1)+1=4n2+4n+1,右边=(2n+1)2=4n2+4n+1,
∴左边=右边,
∴4n(n+1)+1=(2n+1)2;
(3)利用前面的规律,可知
4(
x2+x)(
x2+x+1)+1=(
x2+x+
x2+x+1)2=(x2+2x+1)2=(x+1)4,
即4(
x2+x)(
x2+x+1)+1=(x+1)4.
(2)猜想第n个等式为4n(n+1)+1=(2n+1)2,理由如下:
∵左边=4n(n+1)+1=4n2+4n+1,右边=(2n+1)2=4n2+4n+1,
∴左边=右边,
∴4n(n+1)+1=(2n+1)2;
(3)利用前面的规律,可知
4(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即4(
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了规律型:数字的变化类与完全平方公式,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是得出规律4n(n+1)+1=(2n+1)2.

练习册系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AB=10,△ABC的角平分线AD的长为8,BD=6,求AC的长.
如图,在△ABC中,AB=10,△ABC的角平分线AD的长为8,BD=6,求AC的长.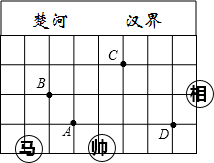 中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图①中“马”所在的位置可以直接走到点A或点B处.
中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图①中“马”所在的位置可以直接走到点A或点B处. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题: