题目内容
18.已知正方形ABCD的对角线AC=3$\sqrt{2}$,则正方形ABCD的周长为12.分析 由正方形的性质知△ABC是等腰直角三角形,已知斜边AC的长,即可求得直角边AB、BC的值,求得了正方形的边长,即可得出正方形的周长.
解答 解:如图所示:
∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2}$AB=3$\sqrt{2}$,
∴AB=3,
∴正方形ABCD的周长=4AB=12.
故答案为:12.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,由勾股定理求出正方形的边长是解决问题的关键.

练习册系列答案
相关题目
6.真命题的个数是( )
①对角线互相平分的四边形是平行四边形.②两组对角线分别相等的四边形是平行四边形.③一组对边平行,另一组对边相等的四边形是平行四边形.④一组邻角相等,另一组邻角互补的四边形是矩形.
①对角线互相平分的四边形是平行四边形.②两组对角线分别相等的四边形是平行四边形.③一组对边平行,另一组对边相等的四边形是平行四边形.④一组邻角相等,另一组邻角互补的四边形是矩形.
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 4个 |
13.下列实数中,是无理数的是( )
| A. | 0 | B. | $\frac{2}{7}$ | C. | 3.141414… | D. | $\sqrt{2}$ |
4.已知x=$\sqrt{2}-5$,则代数式(x+4)2的值为( )
| A. | 3-2$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 1-$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AB=CD,请你再添加个条件,使得AE=DF,并说明理由.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AB=CD,请你再添加个条件,使得AE=DF,并说明理由.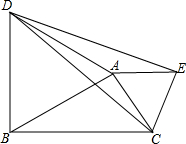 已知,等边△ABD,△ACE,∠BAC=90°,求证:DC=DE.
已知,等边△ABD,△ACE,∠BAC=90°,求证:DC=DE.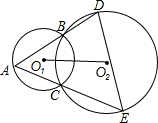 圆O1和圆O2相交于B、C,过圆O1上一点A作AB、AC分别交圆O2于D,E,求证:△ADE的外接圆的半径等于O1O2.
圆O1和圆O2相交于B、C,过圆O1上一点A作AB、AC分别交圆O2于D,E,求证:△ADE的外接圆的半径等于O1O2.