题目内容
11.盒子里装有大小形状相同,质地均匀的4个白球和3个红球,搅匀后从中摸出一个球,放回搅匀后,再摸出第二个球,则两次取出的均是红球的概率是$\frac{9}{49}$.分析 根据题意可以求得每次摸到红球的概率,两次都摸到红球的概率就是两次的概率的乘积,本题得以解决.
解答 解:由题意可得,
第一次摸到红球的概率是:$\frac{3}{7}$,
第二次摸到红球的概率是:$\frac{3}{7}$,
故两次取出的均是红球的概率是:$\frac{3}{7}×\frac{3}{7}=\frac{9}{49}$.
故答案为:$\frac{9}{49}$.
点评 本题考查列表法与树状图法,解题的关键是明确题意,可以求出每次摸到的概率,明确两次都发生的概率就是两次发生的概率的乘积.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
16.-2016的相反数是( )
| A. | -2016 | B. | 2016 | C. | ±2016 | D. | $\frac{1}{2016}$ |
20.若关于x的一元二次方程kx2-2x-1=0没有实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k>1 | D. | k<-1 |
 如图是由几何相同的小正方体搭成的一个几何体,从左边看得到的平面图形是( )
如图是由几何相同的小正方体搭成的一个几何体,从左边看得到的平面图形是( )



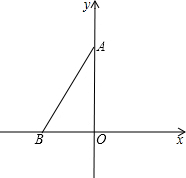 如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).
如图,△AOB在平面直角坐标系中的位置如图所示,点O为坐标原点,∠BAO=30°,点B的坐标为(-1,0),在y的正半轴上找到一点P,使△PAB为等腰三角形,则符合条件的点P的坐标为(0,2+$\sqrt{3}$)或(0,$\frac{\sqrt{3}}{3}$).