题目内容
2.已知点A1(a1,a2),A2(a2,a3),A3(a3,a4),…An(an,an+1),(n为正整数)都在一次函数y=x+3的图象上,若a1=2,则a2016=6047.分析 分别代入y=x+3,得出a2=a1+3,a3=a2+3=a1+6,a4=a3+3=a1+9,…an+1=an+3=a1+3n,依此规律可得a2016=2+3×2015,然后进行有理数计算即可得到答案.
解答 解:∵点A1(a1,a2),A2(a2,a3),A3(a3,a4),…An(an,an+1),(n为正整数)都在一次函数y=x+3的图象上,
∴a2=a1+3,
a3=a2+3=a1+6,
a4=a3+3=a1+9,
…
an+1=an+3=a1+3n
∴a2016=a1+3×2015=6047.
故答案为6047.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.将一个矩形纸片(厚度不计)置于太阳光下,改变纸片的摆放位置和方向,则其留在地面上的影子的形状一定不是( )
| A. | 三角形 | B. | 平行四边形 | C. | 矩形 | D. | 正方形 |
10.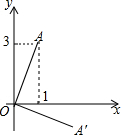 如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
 如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )| A. | $\sqrt{10}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | 1 |
17.下列几何体中,主视图相同的是( )


| A. | ①② | B. | ①④ | C. | ①③ | D. | ②④ |




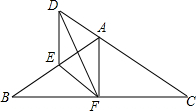 如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.