题目内容
13.在△ABC中,∠ACB=90°,点D是AB边的中点,点E是AC上异于点C的一动点,过C、D、E三点的⊙O交BC与点F,连结CD、DE、DF、EF.(1)△FED与△ABC相似吗?以图1为例说明理由;
(2)若AC=6,BC=8,
①求⊙O半径r的范围;
②如图2,当⊙O与AB相切于点D时,求⊙O半径r的值.
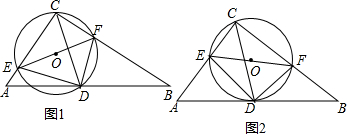
分析 (1)先由直角三角形斜边的中线是斜边的一半,得出等腰三角形,得出∠BCD=∠B,再得出∠BCD=∠FEC,从而判断出结论.
(2)由△FED∽△ABC得出$\frac{EF}{AB}=\frac{DE}{BC}$,计算即可;
(3)先判断出FD=FB,EA=ED,再用勾股定理得出,(6-4x)2+(8-3x)2=(5x)2,计算即可.
解答 解:(1)△FED∽△ABC,
理由:∵∠ACB=90°,点D是AB中点,
∴∠BCD=∠B,
∵在⊙O中,∠BCD=∠FEC,
∴∠FED=∠B,
∵∠ACB=90°,
∴EF为⊙O的直径,
∴∠EDF=90°,
∴∠EDF=∠ACB,
∴△FED∽△ABC;
(2)在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
当点E与点A重合时,EF最长,
由(1)有,△FED∽△ABC
∴$\frac{EF}{AB}=\frac{DE}{BC}$,
∴$\frac{EF}{10}=\frac{5}{8}$,
∴EF=$\frac{25}{4}$,
当圆心O落在CD上时,EF最短,此时EF=CD=$\frac{1}{2}$AB=5,
∴5≤EF≤$\frac{25}{4}$,
∴$\frac{5}{2}$≤r≤$\frac{25}{8}$;
(3)连接OD,
∵⊙O与AB相切与D,
∴∠ODB=90°,
∴∠FDB+∠ODF=90°,
∵△FED∽△ABC,
∴∠EFD=∠A,
∵OD=OF,
∴∠EFD=∠ODF,
∴∠ODF=∠A,
∵∠A+∠B=90°,
∴∠FDB=∠B,
∴FD=FB,
同理:EA=ED,
∵△FED∽△ABC,
∴$\frac{DE}{DF}=\frac{BC}{AC}=\frac{4}{3}$,
设DE=4x,DF=3x,
∴AE=4x,BF=3x,EF=5x,
∴CE=6-4x,CF=8-3x,
根据勾股定理得,(6-4x)2+(8-3x)2=(5x)2,
∴x=$\frac{25}{24}$,
EF=5x=$\frac{125}{24}$,
∴⊙O的半径r为$\frac{125}{48}$.
点评 此题是圆综合题,主要考查了相似三角形的性质和判定,勾股定理,圆周角,解本题的关键是圆中相似三角形条件的判断∠BCD=∠FEC难点是判断EF最长和最短得位置

 阅读快车系列答案
阅读快车系列答案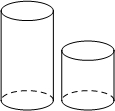 图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )
图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )| A. | 俯视图相同 | B. | 主视图、俯视图、左视图都相同 | ||
| C. | 左视图相同 | D. | 主视图相同 |
 如图所示的立体图形的主视图是( )
如图所示的立体图形的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图为一个几何体三视图,主视图和俯视图都是矩形,则侧面积是( )
如图为一个几何体三视图,主视图和俯视图都是矩形,则侧面积是( )| A. | 8+4$\sqrt{2}$ | B. | 20+8$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
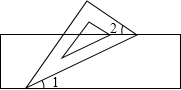 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°. 如图,正方形ABCD的边长为2,DC边在x轴上,DC的中点与坐标原点O重合,点M是x轴上的一个动点,求$\frac{MA}{MB}$的最大值.
如图,正方形ABCD的边长为2,DC边在x轴上,DC的中点与坐标原点O重合,点M是x轴上的一个动点,求$\frac{MA}{MB}$的最大值.