题目内容
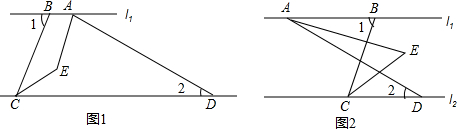
17.如图1,已知l1∥l2,点A,B在直线l1上,点C,D在l2上,连接AD,BC.AE,CE分别是∠BAD,∠BCD的平分线,∠1=70°,∠2=30°.(1)求∠AEC的度数;
(2)如图2,将线段AD沿线段CD方向平移,其他条件不变,求∠AEC的度数.
分析 (1)利用平行线的性质结合角平分线的性质得出∠BAE以及∠AEF的度数即可得出答案;
(2)利用平行线的性质结合角平分线的性质得出∠ECD以及∠AEF的度数即可得出答案.
解答 解:(1)如图1,过点E作EF∥l1,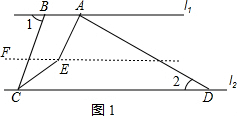
∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠α,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD=$\frac{1}{2}$×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
∵l1∥l2,
∴∠BAD+∠2=180°,
∵∠2=30°,
∴∠BAD=150°,
∵AE平分∠BAD,
∴∠BAE=$\frac{1}{2}$×150°=75°,
∵EF∥l1,
∴∠BAE+∠AEF=180°,
∴∠AEF=105°,
∴∠AEC=105°+35°=140°;
(2)如图2,过点E作EF∥l1,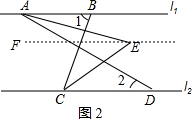
∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠1,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD=$\frac{1}{2}$×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
同理可求∠AEF=15°,
∴∠AEC=∠AEF+∠CEF=50°.
点评 此题主要考查了平移的性质以及角平分线的性质、平行线的性质等知识,正确应用平行线的性质得出各角之间关系是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
8.-27的立方根与9的平方根之和是( )
| A. | 0 | B. | 6 | C. | 0或-6 | D. | -12或6 |
12.下列计算中,正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
2.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是( )
| A. | y=t-0.5 | B. | y=t-0.6 | C. | y=3.4t-7.8 | D. | y=3.4t-8 |
6.2017年4月1日,经中共中央、国务院决定,批准建设国家级新区-雄安新区,据专家预测,雄安新区初始人口约为100万人左右,则1000000用科学记数法表示应为( )
| A. | 1×104 | B. | 1×105 | C. | 1×106 | D. | 1×107 |
7.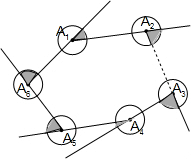 如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
 如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )| A. | πcm2 | B. | 2πcm2 | C. | 2016πcm2 | D. | 2017πcm2 |
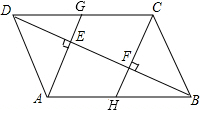 如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H.
如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H. 如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )
如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )


