题目内容
20.解不等式1+$\frac{x+1}{2}$≥2-$\frac{x+7}{3}$,并求出其最小整数解.分析 去分母,去括号,移项,合并同类项,系数化成1,即可得出答案.
解答 解:1+$\frac{x+1}{2}$≥2-$\frac{x+7}{3}$,
去分母,得6+3(x+1)≥12-2(x+7),
去括号,得6+3x+3≥12-2x-14,
移项、合并同类项,得5x≥-11,
系数化为1,得x≥-$\frac{11}{5}$,
故不等式的最小整数解为-2.
点评 本题考查了解一元一次不等式和一元一次不等式的整数解,能求出不等式的解集是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知ax=3,ay=5,则ax+y的值为( )
| A. | 8 | B. | 35 | C. | 15 | D. | 53 |
8.-27的立方根与9的平方根之和是( )
| A. | 0 | B. | 6 | C. | 0或-6 | D. | -12或6 |
12.下列计算中,正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |

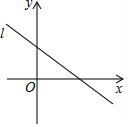 如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )
如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )