题目内容
9．依次连接菱形的四边中点得到的四边形一定是（ ）| A． | 矩形 | B． | 菱形 | C． | 正方形 | D． | 三角形 |
分析 作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半判定出四边形EFGH是平行四边形，再根据菱形的对角线互相垂直可得EF⊥FG，然后根据有一个角是直角的平行四边形是矩形判断．
解答 解：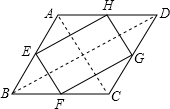
如图，∵E、F分别是AB、BC的中点，
∴EF∥AC且EF=$\frac{1}{2}$AC，
同理，GH∥AC且GH=$\frac{1}{2}$AC，
∴EF∥GH且EF=GH，
∴四边形EFGH是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
又根据三角形的中位线定理，EF∥AC，FG∥BD，
∴EF⊥FG，
∴平行四边形EFGH是矩形．
故选A．
点评 本题主要考查了三角形的中位线定理，菱形的性质，以及矩形的判定，连接四边形的中点得到的四边形的形状主要与原四边形的对角线的关系有关，原四边形的对角线相等，则得到的四边形是菱形，原四边形对角线互相垂直，则得到的四边形是矩形，连接任意四边形的四条边的中点得到的四边形都是平行四边形．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
20．下列说法：（1）有两对边对应相等的两个等腰三角形全等；（2）三个外角都相等的三角形是等边三角形； （3）等腰三角形一边上的中线、高、角的平分线互相重合；（4）两个图形关于某条直线对称，且对应线段相交，交点一定在对称轴上；其中正确的说法有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．
如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②∠B=∠E，BC=EF，∠C=∠F；③AB=DE，∠B=∠E，AC=DF．其中，能使△ABC≌△DEF的条件共有（ ）
如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②∠B=∠E，BC=EF，∠C=∠F；③AB=DE，∠B=∠E，AC=DF．其中，能使△ABC≌△DEF的条件共有（ ）| A． | 0组 | B． | 1组 | C． | 2组 | D． | 3组 |
14．下列计算正确的是（ ）
| A． | $\sqrt{（-4）^{2}}$=2 | B． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C． | $\sqrt{3}•\sqrt{6}=3\sqrt{2}$ | D． | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
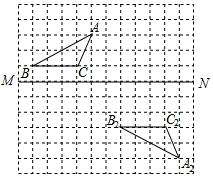在边长为1的正方形网格中，