题目内容
如图，利用标杆BE测量建筑物DC的高度，如果标杆BE长为l.2米，若tanA=| 3 |
| 4 |
| A、6.3米 | B、7.5米 |
| C、8米 | D、6.5米 |
考点：解直角三角形的应用
专题：
分析：通过解直角△AEB求得AB的长度；结合已知条件得到AC的长度；最后通过解直角△ADC来求线段CD的长度即可．
解答：解：如图，∵在△AEB中，∠ABE=90°，BE=1.2米，tanA=
，
∴AB=
=
=1.6（米）．
又∵BC=8.4米，
∴AC=AB+BC=10米．
又∵在直角△ACD中，∠C=90°，tanA=
，
∴CD=AC•tanA=10×
=7.5（米）
故选：B．
| 3 |
| 4 |
∴AB=
| EB |
| tanA |
| 1.2 | ||
|
又∵BC=8.4米，
∴AC=AB+BC=10米．
又∵在直角△ACD中，∠C=90°，tanA=
| 3 |
| 4 |
∴CD=AC•tanA=10×
| 3 |
| 4 |
故选：B．
点评：本题考查了解直角三角形的应用．解直角三角形的一般过程是：
①将实际问题抽象为数学问题（画出平面图形，构造出直角三角形转化为解直角三角形问题）．
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案．
①将实际问题抽象为数学问题（画出平面图形，构造出直角三角形转化为解直角三角形问题）．
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案．
练习册系列答案
相关题目
对于算式
的计算结果，有以下六种说法：①是一个16位整数；②是一个15位整数；③0的个数是14；④0的个数是13；⑤只有两个非0数字；⑥至多有一个非0数字．其中正确的说法是（ ）
| 1.415×3.514×1.8 |
| 0.2×0.729 |
| A、①、③、⑤ |
| B、②、③、⑥ |
| C、②、④、⑥ |
| D、①、④、⑤ |
下列说法不正确的是（ ）
| A、-5是25的平方根 |
| B、1的平方根与立方根相同 |
| C、（-5）2的算术平方根是5 |
| D、-8的立方根是-2 |
下列变形，是因式分解的是（ ）
| A、x（x-1）=x2-x |
| B、x2-x+1=x（x-1）+1 |
| C、x2-x=x（x-1） |
| D、2a（b+c）=2ab+2ac |
为求1+2+22+23+…+22008的值，可令S=1+2+22+23+…+22008，则2S=2+22+23+24+…+22009，因此2S-S=22009-1，所以1+2+22+23+…+22008=22009-1．仿照以上推理计算出1+3+32+33+…+32014的值是（ ）
| A、32015-1 | ||
| B、32014-1 | ||
C、
| ||
D、
|
关于x的方程：x+
=c+
的解是x1=c，x2=
，x-
=c-
解是x1=c，x2=-
，则x+
=c+
的解是（ ）
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x-1 |
| 1 |
| c-1 |
A、x1=c，x2=
| ||
B、x1=c-1，x2=
| ||
C、x1=c，x2=
| ||
D、x1=c，x2=
|
如图，已知点A（0，1），点B（1，0）．点P（t，m）是线段AB上一动点，且0＜t＜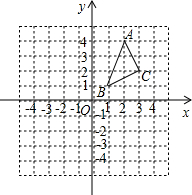
△ABC在平面直角坐标系中的位置如图．A、B、C三点在格点上．