题目内容
18.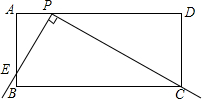 如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E.
如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边经过点C,另一直角边AB交于点E.(1)求证:Rt△AEP∽Rt△DPC;
(2)当∠CPD=30°时,求AE的长;
(3)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
分析 (1)根据矩形的性质,推出∠D=∠A=90°,再由直角三角形的性质,得出∠PCD+∠DPC=90°,又因∠CPE=90°,推出∠EPA+∠DPC=90°,∠PCD=∠EPA,从而证明△CDP∽△PAE;
(2)由△CDP∽△PAE得出∠EPA=∠PCD=30°,由角的正切值定理知AE=AP•tan∠EAP,代入相应的数据即可求得答案;
(3)假设存在满足条件的点P,设DP=x,则AP=11-x,由△CDP∽△PAE知$\frac{CD}{AP}$=2,解得x=8,此时AP=3,AE=4.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠D=∠A=90°,CD=AB=4,
∴∠PCD+∠DPC=90°,
又∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴Rt△AEP∽Rt△DPC;
(2)解:在Rt△PCD中,由tan∠PCD=$\frac{PD}{CD}$,
∴PD=CD•tan∠PCD=4×tan30°=4×$\frac{\sqrt{3}}{3}$,
∴AP=AD-PD=11-$\frac{4\sqrt{3}}{3}$;
解法1:由△CDP∽△PAE知:$\frac{PD}{AE}=\frac{CD}{AP}$,
∴AE=$\frac{PD•AP}{CD}$,
(3)解:假设存在满足条件的点P,
设DP=x,则AP=10-x,
∵△CDP∽△PAE,
根据△CDP的周长等于△PAE周长的2倍,得到两三角形的相似比为2,
∴$\frac{CD}{AP}$=$\frac{4}{10-x}$,
解得x=8.
此时AP=2,AE=4.
点评 此题考查了矩形的性质以及三角形的相似性质以及特殊角的锐角三角函数值,根据△CDP的周长等于△PAE周长的2倍,得到两三角形的相似比为2是解题关键.

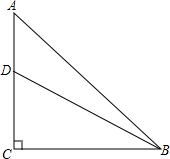 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
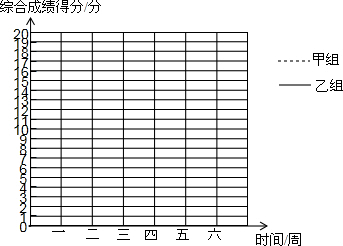 某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:| 周次 | ||||||
| 组别 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲组 | 12 | 15 | 16 | 14 | 14 | 13 |
| 乙组 | 9 | 14 | 10 | 17 | 16 | 18 |
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
| 平均数 | 中位数 | 方差 | |
| 甲组 | 14 | 14 | 1.7 |
| 乙组 | 14 | 15 | 11.7 |
| A. | 75cm,115cm | B. | 60cm,100cm | C. | 85cm,125cm | D. | 45cm,85cm |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,AC⊥CB,DB⊥CB,AB=DC,AB、CD交于点O.求证:OC=OB.
如图,AC⊥CB,DB⊥CB,AB=DC,AB、CD交于点O.求证:OC=OB. 道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?
道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?