有一人患了流感.经过两轮传染后.共有100人患了流感．假设每轮传染中.平均一个人传染了x个人.则依题意可列方程为=100．题目和参考答案——青夏教育精英家教网—

题目内容

1．有一人患了流感，经过两轮传染后，共有100人患了流感．假设每轮传染中，平均一个人传染了x个人，则依题意可列方程为（1+x）+x（1+x）=100．

分析由于每轮传染中平均一个人传染的人数是x人，那么经过第一轮后有（1+x）人患了流感，经过第二轮后有[（1+x）+x（1+x）]人患了流感，再根据经过两轮传染后共有100人患了流感即可列出方程．

解答解：依题意得（1+x）+x（1+x）=100．
故答案为：（1+x）+x（1+x）=100．

点评本题考查了一元二次方程的运用，解此类题关键是根据题意分别列出不同阶段患了流感的人数．

练习册系列答案

12．化简：
（1）（π-2015）⁰+$\sqrt{12}$+|$\sqrt{3}$-2|；
（2）$\sqrt{16}$+$\root{3}{-27}$+3$\sqrt{3}$-$\sqrt{（-3）^{2}}$．

9．

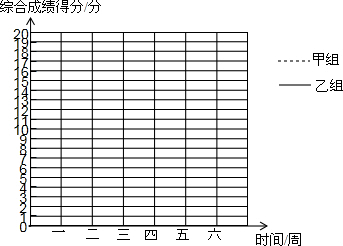某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：

周次
组别	一	二	三	四	五	六
甲组	12	15	16	14	14	13
乙组	9	14	10	17	16	18

（1）请根据上表中的数据完成下表；（注：方差的计算结果精确到0.1）
（2）根据综合评价得分统计表中的数据，请在图中画出甲、乙两组综合评价得分的折线统计图；
（3）由折线统计图中的信息，请分别对甲、乙两个小组连续六周的学习情况做出简要评价．

	平均数	中位数	方差
甲组	14	14	1.7
乙组	14	15	11.7

16．王明同学随机抽查某市10个小区所得到的绿化率情况，结果如下表：

小区绿化率（%）	20	25	30	32
小区个数	2	4	3	1

则关于这10个小区的绿化率情况，下列说法错误的是（　　）

6．两个相似三角形的对应边分别是15cm和25cm，它们的周长相差40cm，则这两个三角形的周长分别是（　　）

13．

如图，AC⊥CB，DB⊥CB，AB=DC，AB、CD交于点O．求证：OC=OB．

10．

道二进行学校规划，工程师需测某教学楼AB的高度，工程师在D得用高2m的测角仪CD，测得楼顶端A的仰角为30°，然后向楼前进30m到达E，又测得教学楼顶端A的仰角为60°，教学楼AB的高时多少？

11．若$\sqrt{-|{x}^{2}-1|}$有意义，则x取值范围为x=±1．

试题分类