题目内容
19．已知x2-4x+4+$\sqrt{{y}^{2}-3}$=0，则x=2，y=$±\sqrt{3}$．分析 直接利用偶次方和算术平方根的性质化简求出即可．
解答 解：∵x2-4x+4+$\sqrt{{y}^{2}-3}$=0，
∴（x-2）2+$\sqrt{{y}^{2}-3}$=0，
则x-2=0，y2-3=0，
解得：x=2，y=±$\sqrt{3}$．
故答案为：2，±$\sqrt{3}$．
点评 此题主要考查了偶次方和算术平方根的定义，正确把握相关定义是解题关键．
练习册系列答案
相关题目
9．
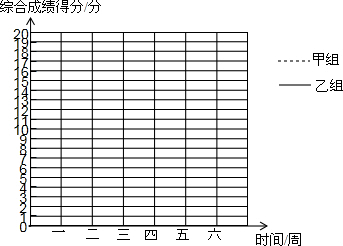某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：
（1）请根据上表中的数据完成下表；（注：方差的计算结果精确到0.1）
（2）根据综合评价得分统计表中的数据，请在图中画出甲、乙两组综合评价得分的折线统计图；
（3）由折线统计图中的信息，请分别对甲、乙两个小组连续六周的学习情况做出简要评价．
某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：| 周次 | ||||||
| 组别 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲组 | 12 | 15 | 16 | 14 | 14 | 13 |
| 乙组 | 9 | 14 | 10 | 17 | 16 | 18 |
（2）根据综合评价得分统计表中的数据，请在图中画出甲、乙两组综合评价得分的折线统计图；
（3）由折线统计图中的信息，请分别对甲、乙两个小组连续六周的学习情况做出简要评价．
| 平均数 | 中位数 | 方差 | |
| 甲组 | 14 | 14 | 1.7 |
| 乙组 | 14 | 15 | 11.7 |
道二进行学校规划，工程师需测某教学楼AB的高度，工程师在D得用高2m的测角仪CD，测得楼顶端A的仰角为30°，然后向楼前进30m到达E，又测得教学楼顶端A的仰角为60°，教学楼AB的高时多少？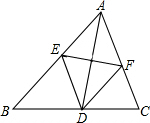
如图，在△ABC中，AD是角平分线，AD的垂直平分线分别交AB、AC于点E、F．