题目内容
11．若m=$\sqrt{32}$×$\sqrt{\frac{1}{2}}$+$\sqrt{20}$，则估计m的取值范围是（ ）| A． | 5＜m＜6 | B． | 6＜m＜7 | C． | 7＜m＜8 | D． | 8＜m＜9 |
分析 先求得$\sqrt{32}$×$\sqrt{\frac{1}{2}}$的值，然后再估算出$\sqrt{20}$的大小从而可确定出m的范围．
解答 解：$\sqrt{32}$×$\sqrt{\frac{1}{2}}$=$\sqrt{16}$=4．
∴m=4+$\sqrt{20}$．
∵16＜20＜25，
∴4＜$\sqrt{20}$＜5．
∴8＜4+$\sqrt{20}$＜9，即8＜m＜9．
故选D．
点评 本题主要考查的是二次根式的乘法和估算无理数的大小，熟练掌握相关知识是解题的关键．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
如图，AB∥CD，CB平分∠ABD，若∠C=35°，则∠D的度数为110°．
如图，△ABC中，AB=AC，D为BC上一点，CD=DE，证明：A、B、D、E四点共圆．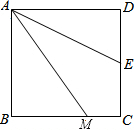
如图，已知四边形ABCD是正方形，M是BC边上一点，E是CD边的中点，AE平分∠DAM．
1．下列根式中属最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{8}$ | D． | $\sqrt{4a+4}$ |