题目内容
已知二次函数y=x2+3x+m(m为常数)的图象与x轴有两个交点,其中一个交点为(-1,0),则另一个交点是( )
| A、(1,0) |
| B、(2,0) |
| C、(-2,0) |
| D、(-3,0) |
考点:抛物线与x轴的交点
专题:
分析:首先求出二次函数y=x2+3x+m(m为常数)的图象的对称轴,然后根据图象与x轴的两个交点关于对称轴对称即可得到答案.
解答:解:设另一个交点坐标为(a,0),
∵y=x2+3x+m,
∴y=x2+3x+
+m-
,
∴y=(x+
)2+m-
,
∴二次函数图象的对称轴为x=-
,
∵
=-
,
∴a=-2,
∴另一个交点是(-2,0),
故选C.
∵y=x2+3x+m,
∴y=x2+3x+
| 9 |
| 4 |
| 9 |
| 4 |
∴y=(x+
| 3 |
| 2 |
| 9 |
| 4 |
∴二次函数图象的对称轴为x=-
| 3 |
| 2 |
∵
| -1+a |
| 2 |
| 3 |
| 2 |
∴a=-2,
∴另一个交点是(-2,0),
故选C.
点评:本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出抛物线图象的对称轴,利用对称知识进行解答,此题难度不大.

练习册系列答案
相关题目
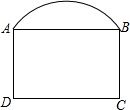 如图,工厂大门由弧线AB和矩形ABCD组成,
如图,工厂大门由弧线AB和矩形ABCD组成,
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①b2-4ac>0;②a+b+c<0;③abc<0;④8a+c>0;⑤方程ax2+bx+c=0的根是x1=-1,x2=3,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①b2-4ac>0;②a+b+c<0;③abc<0;④8a+c>0;⑤方程ax2+bx+c=0的根是x1=-1,x2=3,其中正确结论的个数是( )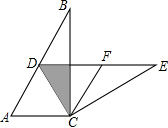 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.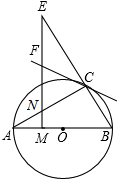 如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E. 如图,点O在∠APB的平分线上,圆O与PA相切于点C.
如图,点O在∠APB的平分线上,圆O与PA相切于点C.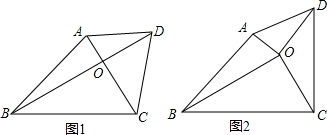
 如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.