题目内容
已知a>b>c,且2a+3b+4c=0.
(1)a+b+c是正数吗?为什么?
(2)若抛物线y=ax2+bx+c在x轴上截得的线段长为
,求抛物线的对称轴.
(1)a+b+c是正数吗?为什么?
(2)若抛物线y=ax2+bx+c在x轴上截得的线段长为
| ||
| 6 |
考点:抛物线与x轴的交点
专题:
分析:(1)一定,2a+3b+4c=(2a+c)+3b+3c<3a+3b+3c=3(a+b+c),即0<3(a+b+c);
(2)根据题意知
=
;
(2)根据题意知
| |x2-x1| |
| 2 |
| ||
| 6 |
解答:解:(1)a+b+c是正数.理由如下:
2a+3b+4c=(2a+c)+3b+3c
∵a>c,
∴2a+c<3a,
∵2a+3b+4c=(2a+c)+3b+3c<3a+3b+3c=3(a+b+c),即0<3(a+b+c),
∴a+b+c>0,即a+b+c是正数;
(2)∵抛物线y=ax2+bx+c在x轴上截得的线段长为
,
∴|x1-x2|=
.
∵x1+x2=-
,x1•x2=
,
∴(x1-x2)2=(x1+x2)2-4x1•x2=
-
=
,
∴
=
,①
又由2a+3b+4c=0得到2a+3b=-4c,②.
由①②得,
+3×
-
=0,
解得,
=
或
=-
,
∴-
=-
或-
=
,
∴该抛物线的对称轴-
或
.
2a+3b+4c=(2a+c)+3b+3c
∵a>c,
∴2a+c<3a,
∵2a+3b+4c=(2a+c)+3b+3c<3a+3b+3c=3(a+b+c),即0<3(a+b+c),
∴a+b+c>0,即a+b+c是正数;
(2)∵抛物线y=ax2+bx+c在x轴上截得的线段长为
| ||
| 6 |
∴|x1-x2|=
| ||
| 6 |
∵x1+x2=-
| b |
| a |
| c |
| a |
∴(x1-x2)2=(x1+x2)2-4x1•x2=
| b2 |
| a2 |
| 4c |
| a |
| 91 |
| 36 |
∴
| b2-4ac |
| a2 |
| 91 |
| 36 |
又由2a+3b+4c=0得到2a+3b=-4c,②.
由①②得,
| b2 |
| a2 |
| b |
| a |
| 19 |
| 36 |
解得,
| b |
| a |
| 1 |
| 6 |
| b |
| a |
| 19 |
| 6 |
∴-
| b |
| 2a |
| 1 |
| 12 |
| b |
| 2a |
| 19 |
| 12 |
∴该抛物线的对称轴-
| 1 |
| 12 |
| 19 |
| 12 |
点评:本题考查了抛物线与x轴的交点.解(2)题时,通过根与系数的关系以及代数式的变形得到方程
+3×
-
=0,可以通过换元法和因式分解法解该方程.
| b2 |
| a2 |
| b |
| a |
| 19 |
| 36 |

练习册系列答案
相关题目
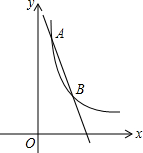 如图,一次函数y=kx+b与反比例函数
如图,一次函数y=kx+b与反比例函数 如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,求证:AF=CE.
如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,求证:AF=CE.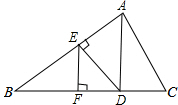 如图,DE⊥AB,EF⊥BC,∠B=∠ADE,试问AD与EF平行吗?请说明你的理由.
如图,DE⊥AB,EF⊥BC,∠B=∠ADE,试问AD与EF平行吗?请说明你的理由.
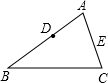 如图,在△ABC中,AB=6,AC=8,D是AB的中点.若在AC上存在一点E,使得△ADE与原三角形相似.
如图,在△ABC中,AB=6,AC=8,D是AB的中点.若在AC上存在一点E,使得△ADE与原三角形相似.