题目内容
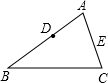如图，在△ABC中，AB=6，AC=8，D是AB的中点．若在AC上存在一点E，使得△ADE与原三角形相似．（1）确定E的位置，并画出简图：
（2）求AE的长．
考点：相似三角形的判定与性质
专题：
分析：（1）分别从△ADE∽△ABC与△ADE∽△ACB去求解，即可画出图形；
（2）分别从当
=
时，△ADE∽△ABC与当
=
时，△ADE∽△ACB去分析求解即可求得答案．
（2）分别从当
| AD |
| AB |
| AE |
| AC |
| AD |
| AC |
| AE |
| AB |
解答：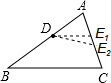
解：（1）画出简图：
（2）∵D是AB的中点，AB=6，
∴AD=3，
∵∠A是公共角，
∴当
=
时，△ADE∽△ABC，
∴
=
，
解得：AE1=4；
∴当
=
时，△ADE∽△ACB，
∴
=
，
解得AE2=
，
∴AE的长为4或
．
解：（1）画出简图：（2）∵D是AB的中点，AB=6，
∴AD=3，
∵∠A是公共角，
∴当
| AD |
| AB |
| AE |
| AC |
∴
| 3 |
| 6 |
| AE |
| 8 |
解得：AE1=4；
∴当
| AD |
| AC |
| AE |
| AB |
∴
| 3 |
| 8 |
| AE |
| 6 |
解得AE2=
| 9 |
| 4 |
∴AE的长为4或
| 9 |
| 4 |
点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
习题精选系列答案
相关题目
