Question

18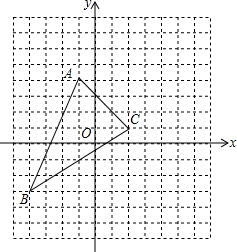．如图，将三角形ABC向右平移5个单位长度，再向上平移3个单位长度，请解答下列问题：
（1）写出点A，B，C的坐标；
（2）画出平移后的三角形A₁B₁C₁；
（3）写出点A₁，B₁，C₁的坐标；
（4）上述平移过程中，各点的横纵坐标均发生了怎样的变化？
（5）三角形ABC的面积是20．

Answer 1

分析 （1）根据平面直角坐标系分别写出点A，B，C的坐标；
（2）首先找出A、B、C三点平移后的位置，再顺次连接即可；
（3）根据平面直角坐标系分别写出A₁，B₁，C₁的坐标；
（4）根据点的坐标可确定各点的横纵坐标均加上了5；
（5）利用矩形的面积减去周围多余三角形的面积可得答案．

解答 解：（1）A（-1，4），B（-4，-3），C（2，1）；

（2）如图所示：

（3）A₁（（4，7），B₁（1，0），C₁（7，4）；

（4）平移后，A、B，C三点的坐标横坐标加上5；

（5）三角形ABC的面积：7×6-$\frac{1}{2}$×7×3-$\frac{1}{2}$×3×3-$\frac{1}{2}$×6×4=20．
故答案为：20．

点评 此题主要考查了平移作图，关键是掌握作平移图形时，找关键点的对应点也是关键的一步．平移作图的一般步骤为：
①确定平移的方向和距离，先确定一组对应点；
②确定图形中的关键点；
③利用第一组对应点和平移的性质确定图中所有关键点的对应点；
④按原图形顺序依次连接对应点，所得到的图形即为平移后的图形．