题目内容
8．
如图所示，直线a、b被直线c所截，现给出下列四种条件：①∠3=∠7，②∠1+∠4=180°，③∠2=∠8，④∠5=∠7，其中能判断是a∥b的条件的序号是（ ）| A． | ①② | B． | ②③ | C． | ①③ | D． | ③④ |
分析 分别利用平行线的判定方法：（1）定理1：两条直线被第三条所截，如果同位角相等，那么这两条直线平行． 简单说成：同位角相等，两直线平行．
（2）定理2：两条直线被第三条所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行．
（3 ）定理3：两条直线被第三条所截，如果同旁内角互补，那么这两条直线平行．简单说成：同旁内角互补，两直线平行，进而得出答案．
解答 解：①当∠3=∠7，则a∥b，故此选项正确；
②当∠4+∠1=180°，无法得到a∥b，故此选项错误；
③∵∠6=∠8，当∠2=∠8，
∴∠2=∠6，故此选项正确；
④当∠5=∠7，无法得到a∥b，故此选项错误．
故选：C．
点评 此题主要考查了平行线的判定，正确把握平行线的判定方法是解题关键．
练习册系列答案
相关题目
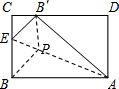如图所示，矩形纸片ABCD中，AB=5，AD=4，将纸片折叠，使点D落在边CB上的D′处，折痕为AE，在折痕AE上存在一点P到边CB的距离与到点D的距离相等，则此相等距离为2.5．
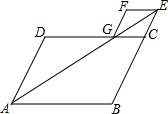如图，在平行四边形ABCD中，∠BAD的平分线交BC的延长线于点E，交CD于点G，过点E作EF∥CD，过点G作FG∥EC，EF，FG交于点F．求证：四边形CEFG为菱形．
如图，在线段AC、BC、CD中，线段CD最短，理由是垂线段最短．
17．下列运算中错误的是（ ）
| A． | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B． | $\sqrt{8}÷\sqrt{2}=2$ | C． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D． | ${（-\sqrt{3}）^2}=3$ |