题目内容
 如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD交⊙O于D,交BC于E,延长BD,AC交于F,G为CD中点,连接OG.
如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD交⊙O于D,交BC于E,延长BD,AC交于F,G为CD中点,连接OG.(1)求证:AE=BF.
(2)若OG•DE=3(2-
| 2 |
考点:圆的综合题
专题:综合题
分析:(1)先证明△ACE与△BCF全等,再利用全等三角形的性质即可证明;
(2)过点O作OH⊥BD于H,根据垂径得BH=DH,则根据三角形中位线性质得AD=2OH,再利用∠CAD=∠BAD得CD=BD,根据弦心距相等,对应的弦相等得到OH=OG,接着证明Rt△BDE∽Rt△ADB,利用相似比得到BD2=AD•DE=2OH•DE=2OG•DE=6(2-
),再利用等腰三角形的判定与性质得DF=BD,AB=AF,即BF=2BD,所以BF2=4BD2=24(2-
),设AC=x,则BC=x,AB=
x=AF,得到CF=AF-AC=(
-1)x,在Rt△BCF中,∵根据勾股定理得[
-1)x]2+x2=24(2-
),解得x=2
或x=-2
(舍去),则AB=
x=2
,于是得到半径OA=
,最后利用圆的面积公式计算即可.
(2)过点O作OH⊥BD于H,根据垂径得BH=DH,则根据三角形中位线性质得AD=2OH,再利用∠CAD=∠BAD得CD=BD,根据弦心距相等,对应的弦相等得到OH=OG,接着证明Rt△BDE∽Rt△ADB,利用相似比得到BD2=AD•DE=2OH•DE=2OG•DE=6(2-
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 6 |
| 6 |
解答:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵∠CAD=∠CBD,
∴∠CAD=∠CBD,
在Rt△ACE和Rt△BCF中,
,
∴Rt△ACE≌Rt△BCF(AAS),
∴AE=BF;
(2)解:过点O作OH⊥BD于H,则BH=DH,
则OH=
AD,即AD=2OH,
又∵∠CAD=∠BAD,
∴CD=BD,
∴OH=OG,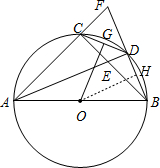
∵∠DBE=∠DAC=∠BAD,
∴Rt△BDE∽Rt△ADB,
∴BD:AD=DE:BD,
∴BD2=AD•DE=2OH•DE=2OG•DE=6(2-
),
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AD⊥BF,
而AD平分∠BAC,
∴AB=AF,
∴BD=FD,
∴BF=2BD,
∴BF2=4BD2=24(2-
),
设AC=x,则BC=x,AB=
x,
∴AF=
x,
∴CF=AF-AC=
x-x=(
-1)x,
在Rt△BCF中,∵CF2+BC2=BF2,
∴[
-1)x]2+x2=24(2-
),
∴x2=12,解得x=2
或x=-2
(舍去),
∴AB=
x=2
,
∴OA=
,
∴⊙O面积=π•(
)2=6π.
∴∠ACB=90°,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵∠CAD=∠CBD,
∴∠CAD=∠CBD,
在Rt△ACE和Rt△BCF中,
|
∴Rt△ACE≌Rt△BCF(AAS),
∴AE=BF;
(2)解:过点O作OH⊥BD于H,则BH=DH,
则OH=
| 1 |
| 2 |
又∵∠CAD=∠BAD,
∴CD=BD,
∴OH=OG,

∵∠DBE=∠DAC=∠BAD,
∴Rt△BDE∽Rt△ADB,
∴BD:AD=DE:BD,
∴BD2=AD•DE=2OH•DE=2OG•DE=6(2-
| 2 |
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AD⊥BF,
而AD平分∠BAC,
∴AB=AF,
∴BD=FD,
∴BF=2BD,
∴BF2=4BD2=24(2-
| 2 |
设AC=x,则BC=x,AB=
| 2 |
∴AF=
| 2 |
∴CF=AF-AC=
| 2 |
| 2 |
在Rt△BCF中,∵CF2+BC2=BF2,
∴[
| 2 |
| 2 |
∴x2=12,解得x=2
| 3 |
| 3 |
∴AB=
| 2 |
| 6 |
∴OA=
| 6 |
∴⊙O面积=π•(
| 6 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和等腰三角形的判定与性质;会应用勾股定理和相似比进行几何计算.

练习册系列答案
相关题目
若不等式组
有解,则a的取值范围是( )
|
| A、a>2 | B、a<2 |
| C、a≤2 | D、a≥2 |
已知m是方程x2+x-1=0的根,则式子3m2+3m+2015的值为( )
| A、2016 | B、2017 |
| C、2018 | D、2019 |
 如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.
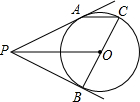 如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.
如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.