题目内容
已知直线y1=
x+1与双曲线y2=
在第一象限交于A点,在第三象限交于B点,直线y1与x轴交于C点.
(1)求A点、B点的坐标;
(2)当x为何值时,y1>y2?
(3)点P是x轴上一个动点,且△APC的面积为3,求P点的坐标.
| 1 |
| 2 |
| 3 |
| 2x |
(1)求A点、B点的坐标;
(2)当x为何值时,y1>y2?
(3)点P是x轴上一个动点,且△APC的面积为3,求P点的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)联立方程,解方程即可求得;
(2)由图象即可求得;
(3)先求得C的坐标,然后设P(x,0),根据三角形的面积公式即可求得.
(2)由图象即可求得;
(3)先求得C的坐标,然后设P(x,0),根据三角形的面积公式即可求得.
解答:解:(1)由
得
或
,
∴A(1,
),B(-3,-
),
(2)由图象可知,当x>1或-3<x<0时,y1>y2;
(3 )∵直线y1=
x+1与x轴交于C点.
∴C点的坐标是(-2,0),
∵△APC的面积为3,若底边为CP,则高为
,设P(x,0)
当P在C点的左边时,CP=-2-x,
CP•
=3,即-2-x=4得x=-6,
∴P1(-6,0);
当P在C点的右边时,CP=x+2,
CP•
=3,即x+2=4得x=2,
∴P2(2,0).
|
|
|
∴A(1,
| 3 |
| 2 |
| 1 |
| 2 |
(2)由图象可知,当x>1或-3<x<0时,y1>y2;
(3 )∵直线y1=
| 1 |
| 2 |
∴C点的坐标是(-2,0),
∵△APC的面积为3,若底边为CP,则高为
| 3 |
| 2 |
当P在C点的左边时,CP=-2-x,
| 1 |
| 2 |
| 3 |
| 2 |
∴P1(-6,0);
当P在C点的右边时,CP=x+2,
| 1 |
| 2 |
| 3 |
| 2 |
∴P2(2,0).
点评:本题考查了一次函数与反比例函数的图象性质、交点问题及函数图象上点的坐标特征.(3)有两种情况分别讨论是重点.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列比较一对数的大小时,正确的是( )
A、-
| ||||
| B、-1.5>-1.4 | ||||
| C、-896>0.01 | ||||
| D、-(+5.5)>-|-4.5| |
若3x-4y=0,则
的值是( )
| x+y |
| y |
A、
| ||
B、
| ||
C、
| ||
D、
|
在-1
,1.2,-2,0,-(-2),(-1)2015中,负数的个数有( )
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
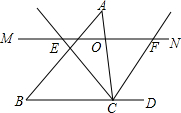 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD交⊙O于D,交BC于E,延长BD,AC交于F,G为CD中点,连接OG.
如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD交⊙O于D,交BC于E,延长BD,AC交于F,G为CD中点,连接OG.