题目内容
13.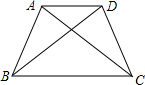 已知AB=CD,AC=BD,说明AD∥BC.
已知AB=CD,AC=BD,说明AD∥BC.提示:(1)先说明△ABC≌△DCB,可推得∠ACB=∠DBC,同理可推得∠CAD=∠BDA.
(2)再说明∠ACB=∠CAD.
分析 先由SSS证明△ABC≌△DCB,得出∠ACB=∠DBC,同理:∠CAD=∠BDA,再根据三角形的外角:∠AOB=∠ACB+∠DBC,∠AOB=∠CAD+∠BDA,得出∠ACB=∠CAD,即可证出AD∥BC.
解答 证明:如图所示: 在△ABC和△DCB中,$\left\{\begin{array}{l}{AB=DC}&{\;}\\{AC=DB}&{\;}\\{BC=CB}&{\;}\end{array}\right.$,
在△ABC和△DCB中,$\left\{\begin{array}{l}{AB=DC}&{\;}\\{AC=DB}&{\;}\\{BC=CB}&{\;}\end{array}\right.$,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,
同理:∠CAD=∠BDA;
∵∠AOB=∠ACB+∠DBC,∠AOB=∠CAD+∠BDA,
∴∠ACB+∠DBC=∠CAD+∠BDA,
∴∠ACB=∠CAD,
∴AD∥BC.
点评 本题考查了全等三角形的判定与性质、三角形的外角性质、平行线的判定;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3.化简:(a+$\frac{3a-4}{a-3}$)(1-$\frac{1}{a-2}$)的结果等于( )
| A. | a-2 | B. | a+2 | C. | $\frac{a-2}{a-3}$ | D. | $\frac{a-3}{a-2}$ |
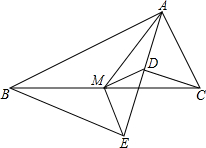 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.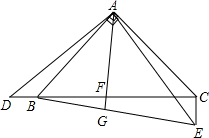 在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.
在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.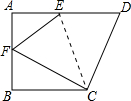 如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.
如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.