题目内容
1.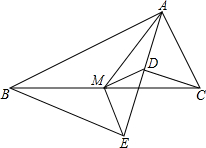 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.(1)若AB=8,AC=4,求MD的长.
(2)求证:MD⊥ME.
分析 (1)延长CD交AB于点F,先证明△ADF≌△ADC,得出AC=AF,CD=DF,再证明MD是△CBF的中位线,得出DM=$\frac{1}{2}$BF=$\frac{1}{2}$(AB-AF),即可得出结果;
(2)连接MF,EF,先证明MF是△ABC的中位线,得出MF∥AC,再证明E、M、F三点共线,得出MD⊥EF,即可得出结论.
解答 解:(1)延长CD交AB于点F;如图1所示: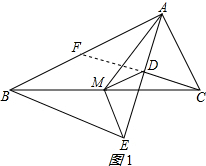
在△ADF和△ADC中,$\left\{\begin{array}{l}{∠FAD=∠CAD}&{\;}\\{AD=AD}&{\;}\\{∠ADF=∠ADC}&{\;}\end{array}\right.$,
∴△ADF≌△ADC(ASA),
∴AC=AF=4,CD=DF,
又∵M是BC的中点,
∴MD是△CBF的中位线,
∴MD∥BF,DM=$\frac{1}{2}$BF=$\frac{1}{2}$(AB-AF)
=$\frac{1}{2}$(AB-AC)=$\frac{1}{2}$(8-4)=2,
(2)证明:连接MF,EF,如图2所示: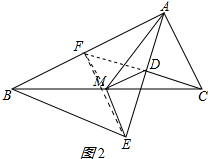 ∵AB=8,AF=4,
∵AB=8,AF=4,
∴F是AB的中点,
∴MF是△ABC的中位线,
∴MF∥AC,
∵AB⊥AC,
∴MF⊥AB,
∵△ABE是等腰直角三角形,
∴EF⊥AB(三线合一),
∴E、M、F三点共线,
∵MD∥AB,
∴MD⊥EF,
∴MD⊥ME.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、三角形中位线定理;本题有一定难度,综合性强,特别是(2)中,需要通过作辅助线证明三点共线才能得出结论.

练习册系列答案
相关题目
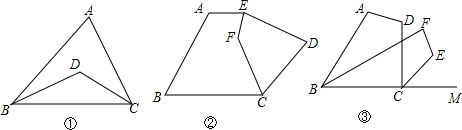
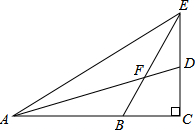 已知Rt△ACE中,AB=CE,BC=DE,∠ACE=90°,求∠AFB的度数.
已知Rt△ACE中,AB=CE,BC=DE,∠ACE=90°,求∠AFB的度数.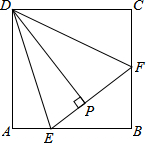 如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.
如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.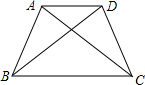 已知AB=CD,AC=BD,说明AD∥BC.
已知AB=CD,AC=BD,说明AD∥BC.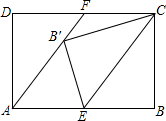 如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.
如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.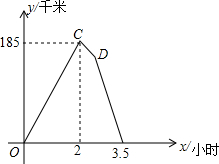 下面的图象反映的过程是:
下面的图象反映的过程是: