题目内容
18.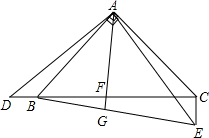 在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.
在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.(1)求证:DB=CE;
(2)点F为DC的中点,连接AF交BE于G,求:∠AGB的度数.
分析 (1)根据∠BAC=90°,EA⊥AD,可得∠BAD=∠CAE,然后根据AB=AC,∠ACE=∠ABD,可证明△ABD≌△ACE,继而可得出DB=CE;
(2)延长AF至M,使FM=AF,连接MC,易证△ADF≌△MCF,可得出AD=AE=CM,易证∠BAE=∠ACM,从而证得△ABE≌△CAM,通过∠ABG=∠CAF,得到∠AGE=90°
解答 证明:(1)∵∠BAC=90°,EA⊥AD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{∠BAD=∠CAE}\\{AB=AC}\\{∠ABD=∠ACE}\end{array}\right.$,
∴△ABD≌△ACE(ASA),
∴DB=CE;
(2)延长AF至M,使FM=AF,连接MC,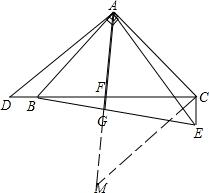
在△ADF与△MCF中,
$\left\{\begin{array}{l}{DF=CF}\\{∠DFA=∠CFM}\\{AF=FM}\end{array}\right.$,
∴△ADF≌△MCF(SAS),
∴AD=CM,
∵△ABD≌△ACE,
∴AD=AE,
∴AD=AE=CM,
∴∠BAM=∠CAM,
在△ABE和△CAM中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠AMC}\\{AE=CM}\end{array}\right.$,
∴△ABE≌△CAM(ASA),
∴∠ABG=∠CAF=45°,
∵∠CAF+∠BAG=90°,
∴∠ABG+∠BAG=90°,
∴∠AGB=∠AGE=90°.
点评 本题考查了全等三角形的判定和性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
8.4的相反数是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | ±4 |
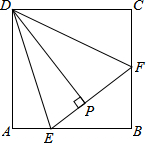 如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.
如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.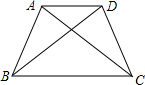 已知AB=CD,AC=BD,说明AD∥BC.
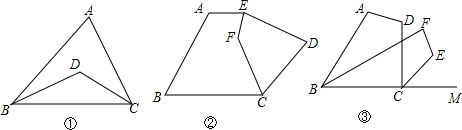
已知AB=CD,AC=BD,说明AD∥BC.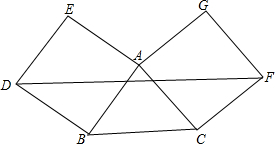 如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC.
如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC.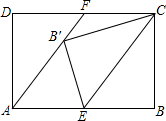 如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.
如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.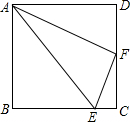 已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.
已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.