题目内容
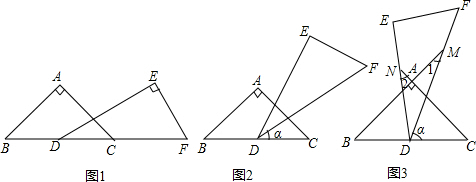
17. 如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )
如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )| A. | 9 | B. | 11 | C. | 14 | D. | 无法确定 |
分析 由DE是边AB的垂直平分线,根据线段垂直平分线的性质,即可得BD=AD.
解答 解:∵DE是边AB的垂直平分线,
∴BD=AD=9.
故选A.
点评 此题考查了线段垂直平分线的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
5.下列结论正确的是( )
| A. | 平行四边形是轴对称图形 | B. | 菱形的对角线互相垂直且相等 | ||
| C. | 正方形的对称轴有4条 | D. | 矩形的对角线互相垂直 |
12.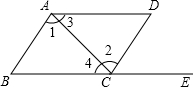 如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
9.下列说法中,正确的有( )
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列计算正确的是( )
| A. | (a-$\frac{1}{2}$b)2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2 | B. | -2a2($\frac{1}{2}$ab+b2)=-a3b+b2a2 | ||
| C. | -$\frac{1}{2}$a2bn•(3anbn+1)=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$ | D. | (a-b)(-a-2b)=-a2-ab+2b2 |
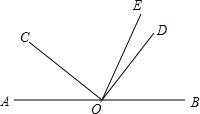 已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC
已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC