题目内容
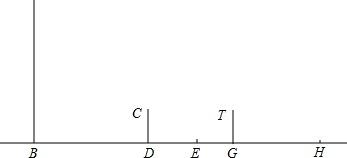
18.如图,花丛中有一路灯AB,在灯光下,小明在D点处的影长DE=3m,沿BD方向走到G点,DG=5m,这时,小明的影长GH=5m,小明的身高为1.7m.(1)画出路灯灯泡A的位置.
(2)求AB的高度.
分析 (1)利用中心投影的性质进而得出A点位置即可;
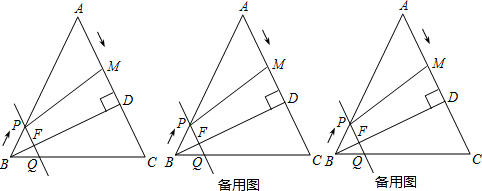
(2)利用相似三角形的判定与性质得出△CDE∽△AEB,同理可得△TGH∽△ABH,进而得出答案.
解答 解:(1)如图所示:A即为所求; ;
;
(2)由题得∠ABD=∠CDE=90°,∠CED=∠AEB
∴△CDE∽△AEB,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$’
同理可得,△TGH∽△ABH,
∴$\frac{TG}{AB}$=$\frac{GH}{BH}$,
∵TG=CD,
∴$\frac{DE}{BE}$=$\frac{GH}{BH}$,
∴$\frac{3}{BD+3}$=$\frac{5}{BD+10}$,
∴BD=7.5(米),
又∵$\frac{CD}{AB}$=$\frac{DE}{BE}$,
∴$\frac{1.7}{AB}$=$\frac{3}{3+7.5}$,
∴AB=5.95(米).
答:AB的高度是5.95米.
点评 此题主要考查了相似三角形的应用以及中心投影的性质,得出△TGH∽△ABH是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,BF∥DE,AE=CF,则△ABF与△CDE全等吗?为什么?
如图,AB∥CD,BF∥DE,AE=CF,则△ABF与△CDE全等吗?为什么?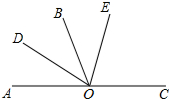 如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.
如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,2∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.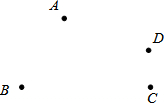 如图,A、B、C、D四点不在同一直线上,读句画图.
如图,A、B、C、D四点不在同一直线上,读句画图.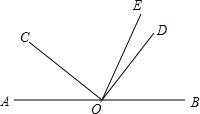 已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC
已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC