在学习了线段的相关知识后.伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠.找到了它的三个四等分点.分别为C.D.E,佳佳再把细绳AB进行折叠.找到了它的两个三等分点.分别为F.G.如图所示.伍伍度量出CF=5厘米.求细绳AB的长度．题目和参考答案——青夏教育精英家教网—

题目内容

4．

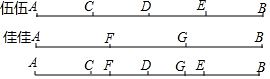在学习了线段的相关知识后，伍伍与佳佳对一根细绳AB进行了如下研究：伍伍把细绳AB折叠，找到了它的三个四等分点，分别为C、D、E；佳佳再把细绳AB进行折叠，找到了它的两个三等分点，分别为F、G，如图所示，伍伍度量出CF=5厘米，求细绳AB的长度．

分析根据三等分、四等分，可得AC，AF，根据线段的和差，可得关于AB的方程，根据解方程，可得答案．

解答解：如图，
由题意，得
AC=$\frac{1}{4}$AB，AF=$\frac{1}{3}$AB．
由线段的和差，得
CF=AF-AC，
即$\frac{1}{3}$AB-$\frac{1}{4}$AB=5，
解得AB=60cm．

点评本题考查了两点间的距离，利用线段的和差得出关于AB的方程是解题关键．

练习册系列答案

同步解析与测评初中总复习指导与训练系列答案

相关题目

x⁵÷x³=x²

（x²）³=x⁵

15．

如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．
求证：△ABM∽△EFA．

12．下列说法中，正确的是（　　）

	A．	0是整数		B．	3.14不是分数
	C．	-（+1）＜+（-2）		D．	倒数等于其本身的数有1，-1，0

2x²+3x³=5x⁵

9．已知三角形两边的长分别是6和12，则此三角形第三边的长可能是（　　）

16．

如图，AE是∠BAC的角平分线，AD⊥BC于点D，若∠B=24°，∠C=36°，则∠DAE的度数是6°．

13．计算与化简；
（1）化简：（$\frac{{a}^{2}}{a+1}$-a+1）÷$\frac{a}{{a}^{2}-1}$再选一个你认为合适的数作为a的值代入求值．
（2）解分式方程：
①$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3
②$\frac{3}{{x}^{2}-9}$+$\frac{x}{x-3}$=1．

14．下面是李刚同学在一次测验中解答的填空题，其中答对的是（　　）

	A．	若x²=4，则x=2
	B．	方程x（2x-1）=2x-1的解为x=1
	C．	若x²+2x+k=0有一根为2，则k=-8
	D．	若分式 $\frac{{{x^2}-x+2}}{x-1}$的值为零，则x=1，2．

试题分类