题目内容
13.计算与化简;(1)化简:($\frac{{a}^{2}}{a+1}$-a+1)÷$\frac{a}{{a}^{2}-1}$再选一个你认为合适的数作为a的值代入求值.
(2)解分式方程:
①$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3
②$\frac{3}{{x}^{2}-9}$+$\frac{x}{x-3}$=1.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a=2代入计算即可求出值;
(2)两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{{a}^{2}-(a+1)(a-1)}{a+1}$•$\frac{(a+1)(a-1)}{a}$=$\frac{1}{a+1}$•$\frac{(a+1)(a-1)}{a}$=a-1,
当a=2时,原式=2-1=1;
(2)①去分母得:1=x-1-3x+6,
解得:x=2,
经检验x=2是增根,分式方程无解;
②去分母得:3+x2+3x=x2-9,
解得:x=-4,
经检验x=-4是原方程的根.
点评 此题考查了解分式方程,以及分式的化简求值,解分式方程利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
8.课本第5页有这样一个定义“三角形的三条中线的交点叫做三角形的重心”.现在我们继续定义:①三角形三边上的高线的交点叫做三角形的垂心;②三角形三条内角平分线的交点叫做三角形的内心;③三角形三边的垂直平分线的交点叫做三角形的外心.在三角形的这四“心”中,到三角形三边距离相等的是( )
| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
18.学校举行广播操比赛,八年级三个班的各项得分及三项得分的平均数如下(单位:分).
根据表中信息回答下列问题:
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
| 服装统一 | 进退场有序 | 动作规范 | 动作整齐 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
5.若8x2my3与-3xy2n是同类项,则|2m-2n|的值是( )
| A. | 0 | B. | 2 | C. | 7 | D. | -1 |
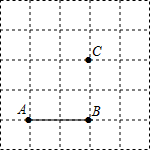 如图,己知线段AB及点C,在方格纸上画图并回答问题.
如图,己知线段AB及点C,在方格纸上画图并回答问题.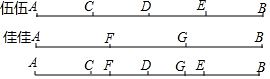 在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度.
在学习了线段的相关知识后,伍伍与佳佳对一根细绳AB进行了如下研究:伍伍把细绳AB折叠,找到了它的三个四等分点,分别为C、D、E;佳佳再把细绳AB进行折叠,找到了它的两个三等分点,分别为F、G,如图所示,伍伍度量出CF=5厘米,求细绳AB的长度. 如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,求∠BPC的大小.
如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,求∠BPC的大小. 请画出由五个正方体组成的如图所示物体的三视图.
请画出由五个正方体组成的如图所示物体的三视图.