题目内容
17.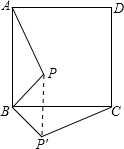 正方形ABCD内一点P,AB=5,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为2$\sqrt{2}$.
正方形ABCD内一点P,AB=5,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为2$\sqrt{2}$.
分析 由旋转的性质得到BP=BP′,且∠PBP′=90°,即三角形BPP′为等腰直角三角形,利用勾股定理求出PP′的长即可.
解答 解:由旋转的性质得到BP=BP′=2,且∠PBP′=90°,
∴△BPP′为等腰直角三角形,
则PP′=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 此题考查了旋转的性质,等腰直角三角形,以及正方形的性质,熟练掌握旋转的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
7.|-9|的值是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
12.己知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的取值范围是( )
| A. | 0<y<l | B. | 1<y<2 | C. | y>6 | D. | 2<y<6 |
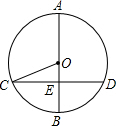 如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.
如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=5.