题目内容
阅读材料:解分式不等式
<0
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①
或②
解①得:无解,解②得:-2<x<1
所以原不等式的解集是-2<x<1
请仿照上述方法解下列分式不等式:
(1)
≤0
(2)
>0.
| 3x+6 |
| x-1 |
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①
|
|
解①得:无解,解②得:-2<x<1
所以原不等式的解集是-2<x<1
请仿照上述方法解下列分式不等式:
(1)
| x-4 |
| 2x+5 |
(2)
| x+2 |
| 2x-6 |
考点:一元一次不等式组的应用
专题:新定义
分析:先把不等式转化为不等式组,然后通过解不等式组来求分式不等式.
解答:解:(1)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①
或②
解①得:无解,
解②得:-2.5<x≤4
所以原不等式的解集是:-2.5<x≤4;
(2)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①
或②
解①得:x>3,
解②得:x<-2.
所以原不等式的解集是:x>3或x<-2.
①
|
|
解①得:无解,
解②得:-2.5<x≤4
所以原不等式的解集是:-2.5<x≤4;
(2)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①
|
|
解①得:x>3,
解②得:x<-2.
所以原不等式的解集是:x>3或x<-2.
点评:本题考查了一元一次不等式组的应用.本题通过材料分析,先求出不等式组中每个不等式的解集,再求其公共部分即可.

练习册系列答案
相关题目
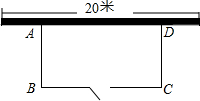 某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围.
某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地,如图,墙长20米,BC边有一个宽为1米的木门(木门用其它材料做不点用竹篱笆).设养鸡场AB边的长为x米,BC边的长为y米,BC的长度不小于10米且不超过墙长.求y关于x的函数解析式及x的取值范围. 如图,四个一样大小的小矩形拼成一个大矩形,如果大矩形的周长为12cm,求小矩形的周长.
如图,四个一样大小的小矩形拼成一个大矩形,如果大矩形的周长为12cm,求小矩形的周长. 如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.
如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 如图,在△ABC中,AF=2BF,CE=3AE,CD=2BD.连接CF交DE于P点,求DP、EP的比值.
如图,在△ABC中,AF=2BF,CE=3AE,CD=2BD.连接CF交DE于P点,求DP、EP的比值. 画出一次函数y=-2x+4的图象,并回答:当函数值为正时,x的取值范围是
画出一次函数y=-2x+4的图象,并回答:当函数值为正时,x的取值范围是