题目内容
12．计算 ${（{1+\sqrt{2}}）^0}+{（{\frac{1}{2}}）^{-1}}+2•cos{30°}$．分析 原式利用零指数幂、负整数指数幂法则，以及特殊角的三角函数值计算即可得到结果．
解答 解：原式=1+2+2×$\frac{\sqrt{3}}{2}$=3+$\sqrt{3}$．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的，若∠BAC=150°，求∠θ的度数．
20．下列不等式中，是一元一次不等式的是（ ）
| A． | 2（1-y）+y＞4y+2 | B． | x（x-5）≥4 | C． | $\frac{1}{2}-\frac{1}{4}＞\frac{1}{5}$ | D． | y+1＜y+2 |
17．在Rt△ABC中，∠C=90°，则下列等式成立的是（ ）
| A． | AB=AC×sinB | B． | BC=AB×sinB | C． | BC=AC×tanB | D． | BC=AC×tanA |
4．
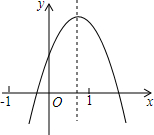已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②2a+b＜0；③4a-2b+c＜0；④b2-4ac＞0，其中正确结论的个数为（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②2a+b＜0；③4a-2b+c＜0；④b2-4ac＞0，其中正确结论的个数为（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
1．在10张奖券中，有4张有奖，从中任抽一张，能中奖的概率为（ ）
| A． | $\frac{4}{10}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
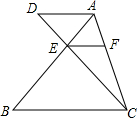如图，AD∥FE∥CB．试探究S△ADC，S△AEC，S△ABC之间的关系，并证明结论．