题目内容
10.计算(1)${(-3)^3}-|{-\frac{1}{2}}|+{(\frac{1}{5})^{-2}}×{(1-\sqrt{3})^0}$
(2)$-{(\frac{b^3}{a})^2}•{(-\frac{2a}{b})^3}÷(-2a{b^4})$
(3)$\frac{x+9}{{{x^2}-9}}-\frac{2}{x-3}$
(4)$\frac{{16-{a^2}}}{{{a^2}+8a+16}}÷\frac{a-4}{2a+8}$.
分析 (1)先算乘方,绝对值,负指数幂与0指数幂,再算加减;
(2)先算乘方,再算乘除;
(3)通分计算即可;
(4)把分子分母因式分解,除法改为乘法约分计算得出答案即可.
解答 解:(1)原式=-27-$\frac{1}{2}$+25×1
=-2$\frac{1}{2}$;
(2)原式=$-\frac{b^6}{a^2}•\frac{{8{a^3}}}{b^3}•\frac{1}{{2a{b^4}}}$
=$-\frac{{8{a^3}{b^6}}}{{2{a^3}{b^7}}}$
=$-\frac{4}{b}$;
(3)原式=$\frac{x+9}{(x+3)(x-3)}-\frac{2}{x-3}$
=$\frac{x+9}{(x+3)(x-3)}-\frac{2(x+3)}{(x+3)(x-3)}$
=$\frac{x+9-2(x+3)}{(x+3)(x-3)}$
=$\frac{x+9-2x-6}{(x+3)(x-3)}$
=$\frac{3-x}{(x+3)(x-3)}$
=$-\frac{1}{x+3}$;
(4)原式=$-\frac{{{a^2}-16}}{{{{(a+4)}^2}}}÷\frac{a-4}{2(a+4)}$
=$-\frac{(a+4)(a-4)}{{{{(a+4)}^2}}}•\frac{2(a+4)}{a-4}$
=-2.
点评 此题考查分式的混合运算,实数的混合运算,掌握运算的顺序与计算的方法是解决问题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
20.下列不等式中,是一元一次不等式的是( )
| A. | 2(1-y)+y>4y+2 | B. | x(x-5)≥4 | C. | $\frac{1}{2}-\frac{1}{4}>\frac{1}{5}$ | D. | y+1<y+2 |
1.在10张奖券中,有4张有奖,从中任抽一张,能中奖的概率为( )
| A. | $\frac{4}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
15.在△ABC中,∠C=90°,AB=2,AC=1,则cosB的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
19.下列关于x的方程中,没有实数根的是( )
| A. | 3x2+4x-2=0 | B. | 2x2+5=6x | C. | 3x2-2$\sqrt{6}$x+2=0 | D. | 2x2+mx-1=0 |
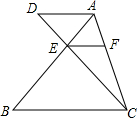 如图,AD∥FE∥CB.试探究S△ADC,S△AEC,S△ABC之间的关系,并证明结论.
如图,AD∥FE∥CB.试探究S△ADC,S△AEC,S△ABC之间的关系,并证明结论.