题目内容
19.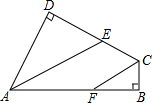 已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
分析 先根据四边形内角和定理得出∠BAD+∠DCB=180°,再由角平分线的定义得出∠DCF=∠BCF,∠DAE=∠BAE,再根据直角三角形的性质可得出∠BFC+∠DCF=BFC+∠BCF=90°,故可得出结论.
解答 解:∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠DCB=180°,
∵AE平分∠BAD,CF平分∠DCB,
∴∠DCF=∠BCF,∠DAE=∠BAE,
∴∠BAE+∠DCF=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠BCD=$\frac{1}{2}$(∠BAD+∠DCB)=90°.
又∵∠BFC+∠DCF=∠BFC+∠BCF=90°,
∴∠BAE=∠BFC,
∴AE∥CF.
点评 本题考查了平行线的判定,角平分线的定义,多边形的内角和,是基础题,难度不大,推出同位角相等是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
 如图,已知一商场自动扶梯的长L为10米,该自动扶梯到达的高度h为6米,自动扶
如图,已知一商场自动扶梯的长L为10米,该自动扶梯到达的高度h为6米,自动扶 如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.
如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上. 某中学的部分学生参加该市中学生知识竞赛,小王同学统计了所有参赛同学的成绩,并且根据学过的知识绘制了统计图(如图).请根据图中提供的信息回答问题:
某中学的部分学生参加该市中学生知识竞赛,小王同学统计了所有参赛同学的成绩,并且根据学过的知识绘制了统计图(如图).请根据图中提供的信息回答问题: