题目内容
2. 如图,直角坐标系中,点P(t,0)是x轴正半轴上的一个动点,过点P作y轴的平行线,分别与直线$y=\frac{2}{3}x$,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴正半轴上的一个动点,过点P作y轴的平行线,分别与直线$y=\frac{2}{3}x$,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.当点(3,0)在正方形ABCD内部时,t的取值范围是$\frac{9}{8}$<t<3.
分析 根据点P的横坐标表示出AB,由点C的横坐标大于3列出不等式求解即可.
解答 解:∵点P(t,0),AB∥y轴,
∴点A(t,$\frac{2}{3}$t),B(t,-t),
∴AB=|$\frac{2}{3}$t-(-t)|=|$\frac{5}{3}$t|,
∵t>0时,点C的横坐标为t+$\frac{5}{3}$t=$\frac{8}{3}$t,
∵点(3,0)在正方形ABCD内部,
∴$\frac{8}{3}$t>3,且t<3,
解得t>$\frac{9}{8}$且t<3,
∴$\frac{9}{8}$<t<3;
故答案为:$\frac{9}{8}$<t<3.
点评 本题是一次函数综合题型,主要利用了一次函数图象上点的坐标特征,正方形的性质;由点C的横坐标大于3列出不等式求解是解题的关键.

练习册系列答案
相关题目
12.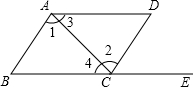 如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠B=∠DCE | D. | ∠D+∠DAB=180° |
9.下列说法中,正确的有( )
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列计算正确的是( )
| A. | (a-$\frac{1}{2}$b)2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2 | B. | -2a2($\frac{1}{2}$ab+b2)=-a3b+b2a2 | ||
| C. | -$\frac{1}{2}$a2bn•(3anbn+1)=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$ | D. | (a-b)(-a-2b)=-a2-ab+2b2 |
11.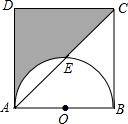 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )| A. | 10-π | B. | 8-π | C. | 12-π | D. | 6-π |
12.下列运算正确的是( )
| A. | a+a2=a3 | B. | -2a-4b=-6ab | C. | (a2)3=a5 | D. | a4÷a2=a2 |
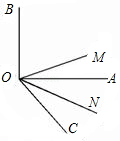 如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.∠AOC=50°,求∠MON的度数.
如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.∠AOC=50°,求∠MON的度数.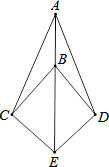 如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.
如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.