题目内容
7．
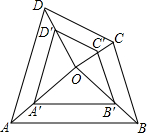如图，点O是四边形ABCD与A′B′C′D′的位似中心，3OA′=2OA，则$\frac{A'B'}{AB}$=$\frac{2}{3}$．
分析 根据位似图形一定相似和相似多边形的性质解答即可．
解答 解：∵3OA′=2OA，
∴$\frac{OA′}{OA}$=$\frac{2}{3}$，
∵四边形ABCD与A′B′C′D′的位似，
∴$\frac{A'B'}{AB}$=$\frac{OA′}{OA}$=$\frac{2}{3}$．
故答案为：$\frac{2}{3}$．
点评 本题考查的是位似变换的性质，如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．下表是国外城市与北京的时差 （带正号的数表示同一时刻比北京时间早的时数）
如果现在东京时间是16：00，那么纽约时间是2：00．（以上均为24小时制）
| 城市 | 纽约 | 巴黎 | 东京 | 多伦多 |
| 时差（时） | -13 | -7 | +1 | -12 |
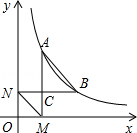如图，已知反比例函数y=$\frac{k}{x}$（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．