题目内容
6.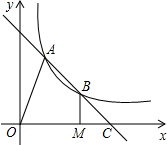 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 过A作AN⊥OC于N,求出ON=MN=CM,设A的坐标是(a,b),得出B(2a,$\frac{1}{2}$b),根据三角形AOC的面积求出ab=4,即可求出答案.
解答 解: 过A作AN⊥OC于N,
过A作AN⊥OC于N,
∵BM⊥OC
∴AN∥BM,
∵,B为AC中点,
∴MN=MC,
∵OM=2MC,
∴ON=MN=CM,
设A的坐标是(a,b),
则B(2a,$\frac{1}{2}$b),
∵四边形OABM的面积为5,
∴S△AOC-S△BCM=5,即$\frac{1}{2}$•3a•b-$\frac{1}{2}$a•$\frac{1}{2}$b=5,
∴ab=4,
∵A在y=$\frac{k}{x}$上,
∴k=ab=4,
故选:B.
点评 本题考查了一次函数和反比例函数的交点问题和三角形的面积的应用,利用图形的面积列方程是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.下列根式中,不能再化简的二次根式是( )
| A. | $\sqrt{{a^2}+1}$ | B. | -$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
15.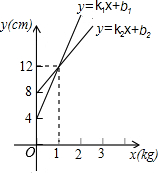 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
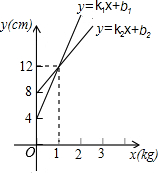 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
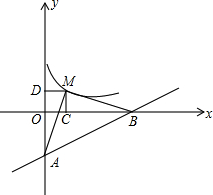 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.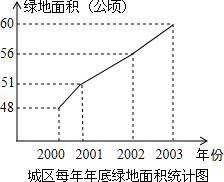 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).