题目内容
17.计算(1)$\sqrt{32}-\sqrt{1\frac{1}{8}}+\sqrt{12\frac{1}{2}}$
(2)4$\sqrt{3}$-2(1-$\sqrt{3}$)+$\sqrt{{{(-2)}^2}}$
(3)$\frac{\sqrt{12}×\sqrt{15}}{\sqrt{3}}$-$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{5}}$
(4)$({\sqrt{5}×\sqrt{6}-2\sqrt{15}})÷\sqrt{15}$
(5)$\frac{1}{{1+\sqrt{2}}}+\frac{1}{{\sqrt{2}+\sqrt{3}}}+\frac{1}{{\sqrt{3}+\sqrt{4}}}+…+\frac{1}{{\sqrt{99}+\sqrt{100}}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先根据二次根式的性质化简,然后合并即可;
(3)根据二次根式的乘除法则运算;
(4)根据二次根式的乘除法则运算;
(5)先分母有理化,然后合并即可.
解答 解:(1)原式=4$\sqrt{2}$-$\frac{3\sqrt{2}}{4}$+$\frac{5\sqrt{2}}{2}$
=$\frac{23\sqrt{2}}{4}$;
(2)原式=4$\sqrt{3}$-2+2$\sqrt{3}$+2
=6$\sqrt{3}$;
(3)原式=$\sqrt{\frac{12×15}{3}}$-($\sqrt{\frac{20}{5}}$+1)
=2$\sqrt{15}$-(2+1)
=2$\sqrt{15}$-3;
(4)原式=$\sqrt{5×6×\frac{1}{15}}$-2$\sqrt{15×\frac{1}{15}}$
=$\sqrt{2}$-2;
(5)原式=$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$
=$\sqrt{2}$-1+$\sqrt{3}$-1+…+$\sqrt{100}$-$\sqrt{99}$
=$\sqrt{100}$-1
=10-1
=9.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
9.下列说法正确的是( )
| A. | 等弧所对的圆心角相等 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 经过三点可以作一个圆 | |
| D. | 相等的圆心角所对的弧相等 |
6.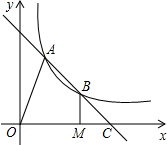 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.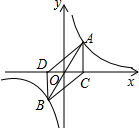 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
 如图,在矩形纸片ABCD中,AB=8,BC=6,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点F处,求AE长.
如图,在矩形纸片ABCD中,AB=8,BC=6,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点F处,求AE长.