题目内容
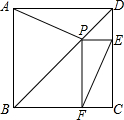 如图,P是正方形ABCD对角线BD上一动点,PE⊥DC,PF⊥BC,E、F分别为垂足,
如图,P是正方形ABCD对角线BD上一动点,PE⊥DC,PF⊥BC,E、F分别为垂足,(1)若CF=3,CE=4,求AP的长.
(2)若AB=8,直接写出EF的最小值为
考点:正方形的性质,全等三角形的判定与性质,矩形的判定与性质
专题:
分析:(1)设正方形ABCD的边长为a,作PF延长线交AD于Q,易证四边形DEPQ为正方形,根据线段之间的数量关系可求出a的值,进而求出AQ的长,利用勾股定理即可求出AP的长;
(2)连结PC,易证△ABP≌△CBP,利用全等三角形的性质可得AP=PC,再证明四边形PECF是矩形,由矩形的性质对角线相等可得PC=EF,所以EF的最小值即为AP的值,问题的解.
(2)连结PC,易证△ABP≌△CBP,利用全等三角形的性质可得AP=PC,再证明四边形PECF是矩形,由矩形的性质对角线相等可得PC=EF,所以EF的最小值即为AP的值,问题的解.
解答:解:(1)设正方形ABCD的边长为a,
作PF延长线交AD于Q,则四边形DEPQ为正方形,
∴PQ=DQ=3,
∵PQ=FQ-PF,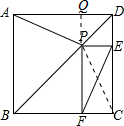
即a-4=3,
∴a=7,
即 AD=7,
∴AQ=AD-DQ=4,
∴AP=
=5
(2)连结PC,
∵四边形ABCD是正方形,BD为对角线,
∴∠BCD=90°,AB=BC,∠ABP=∠CBP,
又∵BP=BP,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,
∵PE⊥DC,PF⊥BC,
∴∠PFC=∠PEC=∠BCD=90°,
∴四边形PFCE是矩形,
∴PC=FE,
∴EF=AP=5,
故答案为:5.
作PF延长线交AD于Q,则四边形DEPQ为正方形,
∴PQ=DQ=3,
∵PQ=FQ-PF,

即a-4=3,
∴a=7,
即 AD=7,
∴AQ=AD-DQ=4,
∴AP=
| 32+42 |
(2)连结PC,
∵四边形ABCD是正方形,BD为对角线,
∴∠BCD=90°,AB=BC,∠ABP=∠CBP,
又∵BP=BP,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴AP=PC,
∵PE⊥DC,PF⊥BC,
∴∠PFC=∠PEC=∠BCD=90°,
∴四边形PFCE是矩形,
∴PC=FE,
∴EF=AP=5,
故答案为:5.
点评:本题考查了正方形的判定和性质、矩形的判定和性质、全等三角形的判定和性质、勾股定理的运用,题目的综合性较强,解题的关键是作辅助线构造全等三角形.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E.
如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E. 已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么?
已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么? 如图,已知直线AB及AB外一点C,过点C作直线EF∥AB(要求:不写作法,保留作图痕迹)
如图,已知直线AB及AB外一点C,过点C作直线EF∥AB(要求:不写作法,保留作图痕迹)