题目内容
16.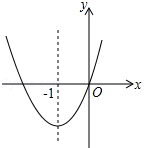 如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )
如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由抛物线的开口向上,对称轴在y轴左侧,判断a,b与0的关系,得到?ab>0,即可判断①;由x=1时,得到y=a+b+c>0,即可判断②;根据对称轴和抛物线与x轴的一个交点,得到另一个交点,然后根据图象即可判断③.
解答 解:①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0
∴?ab>0;故①正确;
②∵观察图象知;当x=1时y=a+b+c>0,
∴②正确;
③∵抛物线的对称轴为x=-1,与x轴交于(0,0),
∴另一个交点为(-2,0),
∴当-2<x<0时,y<0;故③正确;
故选D.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
4.小芳连续5天测得最低气温并整理后得出下表,
由于不小心被墨迹污染了两个数据,这两个数据分别是4,$\sqrt{2}$.
| 日期 | 一 | 二 | 三 | 四 | 五 | 标准差 | 平均气温 |
| 最低气温(℃) | 1 | 3 | 2 | 5 |  |  | 3 |
8.在频率分布直方图中,以下说法错误的是( )
| A. | 每个小长方形的面积等于频数 | B. | 每个小长方形的面积等于频率 | ||
| C. | 频率=$\frac{频数}{数据总数}$ | D. | 各个小长方形面积和等于1 |
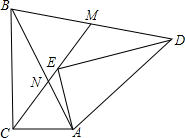 如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.
如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.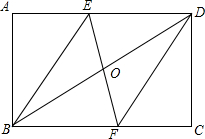 如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论.
如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论.