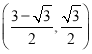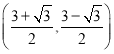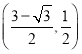题目内容
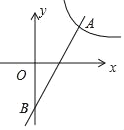
【题目】如图在平面直角坐标系xOy中，一次函数y＝2x﹣2的图象与函数y＝
（k≠0）的图象有交点为A（m，2），与y轴交于点B
（1）求反比例函数的解析式；
（2）若函数y＝在第一象限的图象上有一点P，且△POB的面积为6，求点P坐标．
【答案】（1）
；（2）（6，
）．
【解析】
（1）通过一次函数求出m，即求出A的坐标；然后通过把A坐标代入反比例函数，求反比例函数解析式；
（2）先确定△POB的面积以OB为底，CP为高；OB的长是固定的，只需要CP的长度；点P 在反比例函数图象上，将它代入反比例函数，从而求出P（x，
）即CP＝x； 从而列出S△POB＝
OB·
＝
＝6，即x＝6，并求出y值，从而确定P的坐标；
解：（1）由已知得点A（m，2）在函数y＝2x﹣2图象上，故2m﹣2＝2，解得m＝2，即A（2，2）
并且点A（2，2）也在函数y＝
的图象上，
∴2＝
解得k＝4，∴所以反比例函数y＝
（2）过点P作CP⊥y轴；△POB的面积以OB为底，CP为高；
在函数y＝2x﹣2中，当x＝0时，y＝﹣2
即OB＝2，设函数y＝（x＞0）图象上点P（x，）
∴S△POB＝OB·＝＝6
解得：x＝6，则y＝
∴此时点p（6，
）．
练习册系列答案
名校课堂系列答案
相关题目
