Question

【题目】如图，在平面直角坐标系中，二次函数交轴于点、，交轴于点，在轴上有一点，连接.

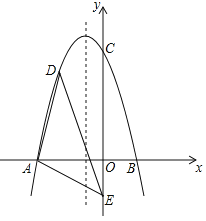
（1）求二次函数的表达式；

（2）若点为抛物线在轴负半轴上方的一个动点，求面积的最大值；

（3）抛物线对称轴上是否存在点，使为等腰三角形，若存在，请直接写出所有点的坐标，若不存在请说明理由.

Answer 1

【答案】（1）二次函数的解析式为；（2）当时，的面积取得最大值；（3）点的坐标为，，.

【解析】（1）把已知点坐标代入函数解析式，得出方程组求解即可；

（2）根据函数解析式设出点D坐标，过点D作DG⊥x轴，交AE于点F，表示△ADE的面积，运用二次函数分析最值即可；

（3）设出点P坐标，分PA=PE，PA=AE，PE=AE三种情况讨论分析即可．

（1）∵二次函数y=ax2+bx+c经过点A（﹣4，0）、B（2，0），C（0，6），

∴，

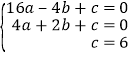解得：，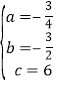

所以二次函数的解析式为：y=；

（2）由A（﹣4，0），E（0，﹣2），可求AE所在直线解析式为y=，

过点D作DN⊥x轴，交AE于点F，交x轴于点G，过点E作EH⊥DF，垂足为H，如图，

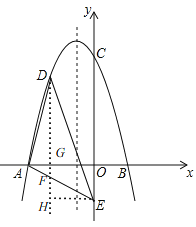
设D（m，），则点F（m，），

∴DF=﹣（）=，

∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH

=×DF×AG+×DF×EH

=×4×DF

=2×（）

=，

∴当m=时，△ADE的面积取得最大值为．

（3）y=的对称轴为x=﹣1，设P（﹣1，n），又E（0，﹣2），A（﹣4，0），可求PA=，PE=，AE=，分三种情况讨论：

当PA=PE时，=，解得：n=1，此时P（﹣1，1）；

当PA=AE时，=，解得：n=，此时点P坐标为（﹣1，）；

当PE=AE时，=，解得：n=﹣2，此时点P坐标为：（﹣1，﹣2）．

综上所述：P点的坐标为：（﹣1，1），（﹣1，），（﹣1，﹣2）．